 |
 |
AbstractSpread is a major parameter in the steel wire rod rolling process since it is required for the calculation of material cross-sectional area and other rolling characteristics. Therefore, it is important to have a method to predict the spread with high accuracy and less computation time in wire rod rolling. In this study, multiple artificial intelligence (AI) methods including Multi-Layer Perceptron (MLP) and Adaptive Neuro-Fuzzy Inference Systems (ANFIS) are employed to predict the spread. The 3D finite element (FE) analysis is used to generate the input data for the AI model and investigate the effect of different input parameters on the spread in one-stand and three-stand rolling setups of the wire rod rolling. The results demonstrate that the backward tension and the roll diameter are the most influencing parameters. Due to the use of dimensionless inputs and outputs, the model is independent of geometries and processing conditions which results in the transferability of the model. Furthermore, the ANFIS model provides some level of reasoning for the user by using a rule-based approach. Data fusion is also used to combine all outputs of the trained models and provide a single output for the prediction of spread in new data sets. The reasoning and transferability of the model result in the prediction of spread for a wide range of conditions in the steel wire rod rolling process. The generality and accuracy of the proposed approach are examined by comparing the results of the AI model with the FE analysis and experimental data obtained from the steelmaking company. The findings indicate that there is good agreement between the predicted and the measured values.
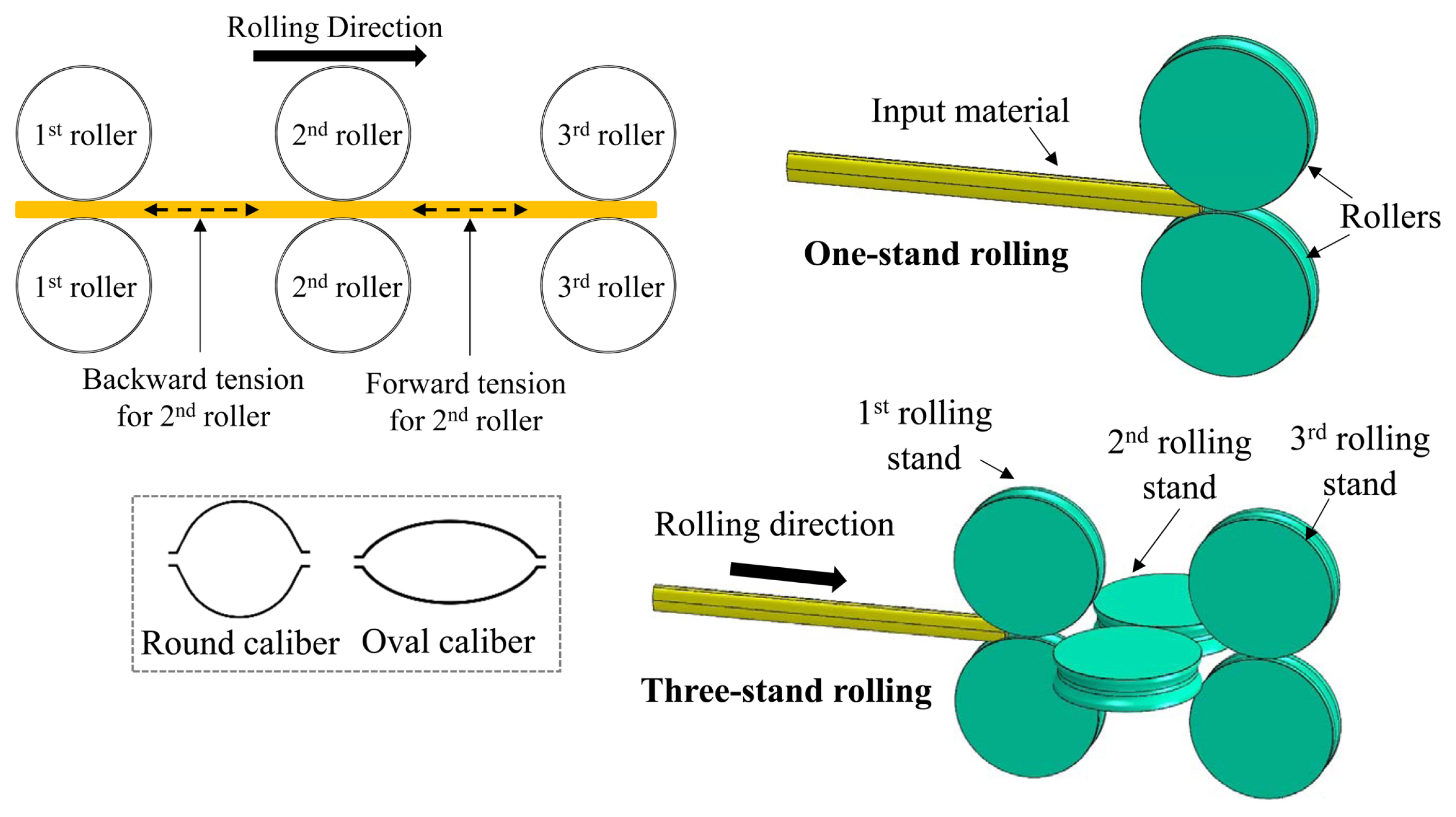
Rolling is one of the most widely used forming processes in a steelmaking company. One of the products of the rolling process is the steel wire rod which is a long semi-finished product with a round cross-section that has several applications in automotive, construction, and other industries. During the manufacturing process of steel wire rods, the initial billet is heated up to around 1,000┬░C and passed through many rolling stands. There are some types of rolling stands with different numbers of rollers, and different roll pass types. A two-roll stand with round-oval and oval-round passes is one of the most common types of rolling setup. Each stand is responsible for a part of the deformation. Thus, the large cross-section of the initial input material is decreased by passing through different rolling stands and a long steel product with a small round cross-section is produced at the end of the process [1,2].
Prediction of the material cross-section after each stand of the rolling is of great importance in industrial applications since it leads to an accurate and optimized pass design and set up of production lines. In addition, it is necessary to have the cross-section of a sample to calculate strain, strain rate, and other parameters in the rolling process [3,4]. Therefore, there has been a great interest to find a reliable method that can quickly and accurately predict the material cross-section in the wire rod rolling process. Maximum spread in wire rod rolling is defined as the maximum increase of material width in the lateral direction after rolling. By having the maximum spread, it is possible to calculate the cross-sectional geometry of the material after the wire rod rolling process [5].
Up to now, several FE analysis studies were performed to investigate the roll force, material deformation, strain distribution, strain homogeneity, caliber design, and temperature distribution in wire rod rolling [6ŌĆō10]. Due to the 3D deformation of the material in wire rod rolling, 3D FE analysis is used, however, in flat rolling the deformation of the material is in the 2D state which represents the plain strain condition [6]. Even though FE analysis is a powerful tool to study several parameters of the rolling process, the long processing time of the simulation is a serious drawback in industrial applications due to the high number of rolling mills (more than 100) in a wire rod production process.
On the other hand, empirical models which can be obtained based on experiments are applicable in industrial applications because of their simplicity. The major problem of empirical models is the generality of these equations since they are normally applicable for a specific range and the results may also be affected by the employed machines and other experimental factors. In addition, it is diff icult, time-consuming, and expensive to experimentally investigate different conditions and parameters such as friction and tension in the rolling process. Therefore, some parameters are not considered in the empirical equations for the prediction of spread in single and multiple rolling stands. Some of the important empirical models in the flat and wire rod rolling process belong to Siebel [11], Wusatowski [12], Saito [13,14], and Shinokura [3] which are mainly based on experimental investigations. ShinokuraŌĆÖs model is used in some industrial applications to predict the spread in the wire rod rolling process due to its simplicity. However, this model mainly considers the geometrical parameters and when some conditions such as velocity, friction, and tension are changed, the error in the predicted spread increases. In addition, there is a coeff icient (╬▒) in ShinokuraŌĆÖs model that directly affects the spread; however, there is no standard approach to select the correct value for this factor since it needs to be changed when some input parameters of the rolling process are changed.
Another approach that has attracted great attention in different industries is based on artif icial intelligence. In the rolling processes, most previous studies are focused to predict the rolling force [15,16], rolling torque [17,18], bending force [19,20], thickness [21], mechanical properties [22,23], and flatness [24,25] in the flat rolling process. However, there are not any comprehensive studies about the prediction of spread in steel wire rod rolling based on artificial intelligence.
Therefore, a method that can predict the spread in wire rod rolling with low computation time, high accuracy, and generality is favorable for industrial applications. To overcome the challenges of the previous studies, the following objectives are set out. First, finite element (ABAQUS/ExplicitTM) software is used to simulate different cases of the 3D wire rod rolling process and investigate the relationship between the input parameters and the output. Second, all the input and output parameters are changed to dimensionless values in which they are not related to a specific rolling stand, so the proposed model can be transferred to other setups and some level of transferability can be achieved which increases the generality of the model. Third, multiple AI methods including MLP and ANFIS are employed to predict the output based on the dimensionless data obtained from FE analysis which results in an accurate and robust prediction. Forth, some level of reasoning is provided for the user by using the ANFIS, thus, the effect of different input parameters can be understood. In addition, data fusion is employed to combine the result of trained MLP and ANFIS models for the prediction of those cases that are out of the range of simulations, thus, the reliability and explainability of this model will be increased.
This study presents a fusion of AI methods to predict the spread in the steel wire rod rolling process. FE analysis is used to simulate several cases to generate the required data for the AI model and find the relationship between inputs and output. For the AI model, MLP is selected since it is a universal approximator and can model any functions regardless of the level of complexity and ANFIS is chosen since it is a rule-based system and provides reasoning [26,27]. The outputs of all trained models for the prediction of some cases which are out of the range of FE analysis are fused to increase the accuracy and robustness of the prediction system. Finally, the proposed model is examined based on the FE analysis data and obtained experimental data from a steelmaking company to verify its performance and capability in industrial applications.
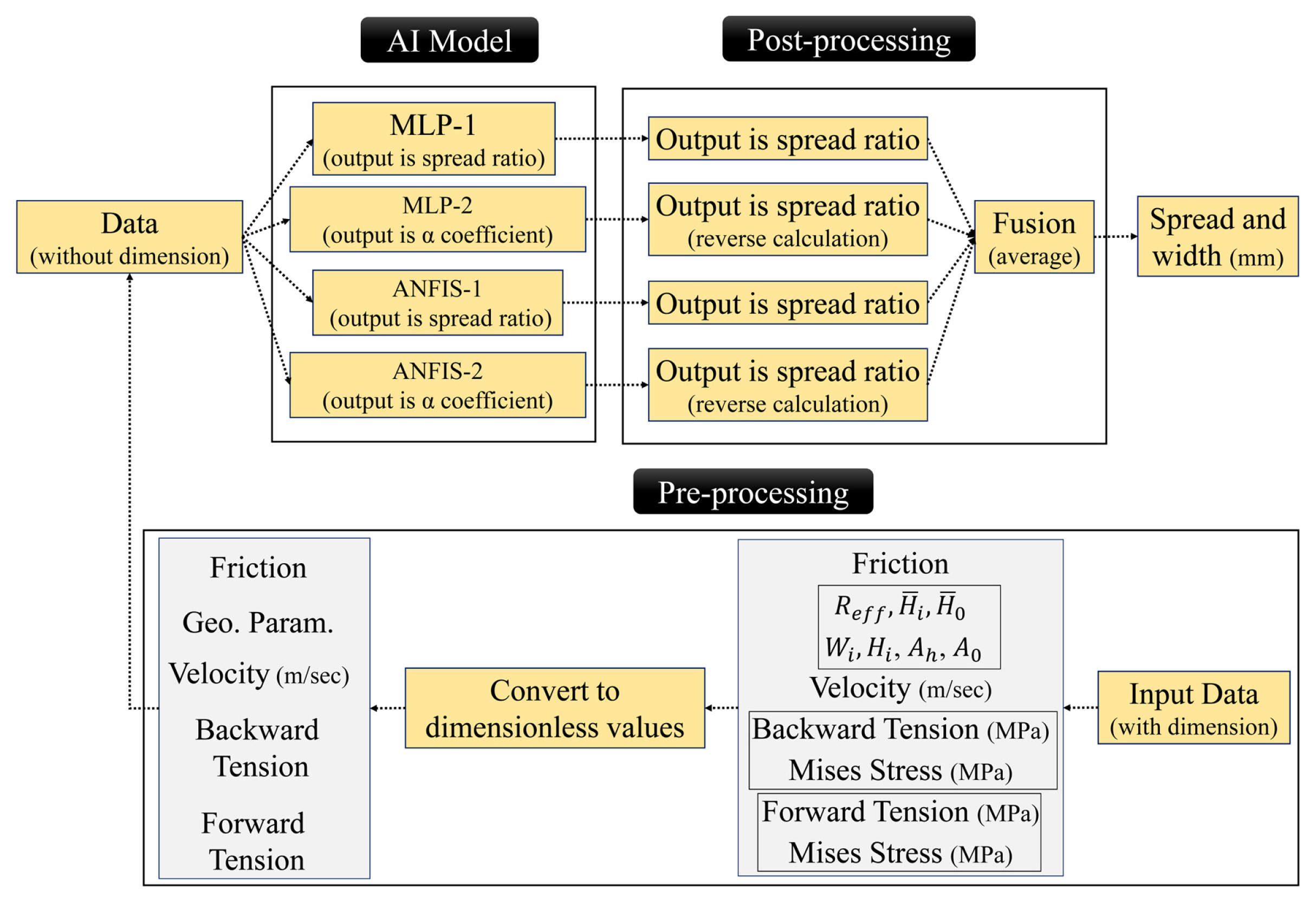
The proposed model to predict the spread in steel wire rod rolling is shown in Fig. 1. This model can be divided into four steps. In the first step, the generated data by FE analysis are considered as the inputs. In the second step, the input data are changed to dimensionless values and then normalized to decrease the effect of the size on the final output. In the third step, all the data pass through the AI method including MLP and ANFIS, and all the outputs are fused together. In the last step, the predicted value is changed to the spread and then the maximum width of the material is determined. Therefore, the width of rolled material can be predicted by the proposed AI-based model.
FE analysis is used to simulate the wire rod rolling process and generate data for the AI model. Due to the existence of 3D deformation, complex contact conditions, and elevated temperature in the wire rod rolling, a 3D coupled thermo-mechanical analysis is performed by using ABAQUS/ ExplicitTM to simulate the steel wire rod rolling process [28,29]. Based on the symmetry of the rollers and billet, only a quarter of them are modeled to decrease the simulation time. In addition, material density is increased artificially by using a fixed mass scaling factor to increase the computational efficiency of the simulations. A mass scaling factor of 16 is considered after increasing the mass scaling factor from 1 to 1,000 and comparing the results of FE analysis in terms of the deformation, stress, kinetic and internal energies [30].
An 8-node coupled thermo-mechanical element (C3D8RT) with reduction integration and hourglass control is used to mesh the material [29,31]. The rigid body constraint and isothermal condition are applied to the roller, and the material is considered a deformable body. Johnson-Cook (JC) material model with the following equation is used to predict material behavior under different conditions [32].
where ╔ø is the equivalent plastic strain, ╬Ą╠ć is the strain rate, ╬Ą╠ćref is the reference strain rate, Tref is the reference temperature, Tm is the melt temperature, A, B, C, n, and m are the five material constants [32]. The JC parameters of the employed steel are shown in Table 1. Since the effect of radiation and convection is negligible in the rolling process, it is assumed that conduction is the main factor for heat loss in the current work [33]. The other parameters which are used for the simulation are shown in Table 2.
The FE analysis part aims to generate data for the prediction system and to investigate the effect of different input parameters on the output. The input parameters are defined as friction, material temperature, roller rotational speed, roll gap, input material size, roller diameter, material strength, backward tension, forward tension, caliber type, and the output parameter is the spread ratio which means the relative difference between initial and final width of material. To design the simulation cases, two setups are considered which are one-stand and three-stand rolling operations; the geometry of the caliber is also considered as oval and round calibers which is shown in Fig. 2. A reference condition is considered for each type of caliber and the input parameters are changed over a specific range. These ranges are selected wide enough to include all the possible cases which may occur in real world rolling operations. The level of changes for each input parameter is shown in Table 3. As an example, the reference condition and the range of input parameter changes only for the oval caliber is shown in Table 4.
For instance, the roll gap in one-stand rolling with oval caliber is changed up to five levels which means the roll gap is changed five times over the range of 5.95 to 11.03 mm (roll gap = 5.95, 7.225, 8.5, 9.775, 11.03 mm) while the other input parameters are kept constant. Thus, the effect of a specific parameter can be understood independently. The same approach is used for other input parameters such as temperature, speed, and so on. These cases are only for one-stand rolling with the oval caliber and for one-stand rolling with the round caliber the same method is used but the range of changes of inputs and the reference condition are different.
In simulations with three-stand rolling, the effect of backward and forward tensions on the spread ratio is studied (Table 5). The rotational speed of the first and third roller is changed, as a result, the backward and forward tensions in three-stand rolling are changed and the effect of the interstand tension on the spread ratio can be investigated. For instance, the speed of the first roller in three-stand rolling (Round-Oval-Round calibers) is changed at five levels (17.97, 18.44, 19.91, 19.391, and 19.86 rev./min), thus, the backward tension is changed at five levels and its effect can be understood; the same method is used to change the speed of the third roller and investigate the effect of forward tension while the speed of the first roller is kept constant. The same approach is used for the other setup of three-stand rolling (Oval-Round-Oval calibers). The reference friction coeff icient is 0.4 for all cases. To consider more cases for the training, all the simulations for one-stand and three-stand rolling are repeated with two other friction coeff icients (╬╝ = 0.25 and 0.3).
FE analysis is used to simulate different cases of wire rod rolling. Due to the use of different case studies, the effect of all input parameters on the output is investigated and the parameters without any significant effect on the output are removed from the training data set. The total number of training data for oval and round caliber is around 300 cases.
One of the most important parts of an AI model is the preprocessing since it can be used to increase the quality of the data and the transferability of the model. The initial values of inputs and outputs describe limited conditions in the wire rod rolling process. If these data are used for the training section, the generality of the prediction model will be a challenging issue since the trained model cannot be used for other rolling stands that have different geometries and processing conditions.
In this part, the initial raw data are processed to make the data easier to interpret for the MLP and ANFIS models. Furthermore, the other aim of preprocessing for this study is to make the data independent of dimensions which results in the transferability of the model. Thus, the prediction model which is trained based on the results of simulations in specific dimensions and processing conditions of wire rod rolling can be used for other dimensions and processing conditions which increases the generality of the proposed model. By examining some equations from the literature [3,11,34], ShinokuraŌĆÖs model is considered for converting the dimensional parameters to dimensionless values. ShinokuraŌĆÖs equation is as follows:
where
In the next step, normalization is used to scale the dimensionless data to a specific range. There are some methods such as linear min-max, z-score, and decimal scaling which are normally used in the preprocessing section. In this study, the following linear formula is used for min-max normalization:
where X is the original data, Xmin is the minimum value of X, Xmax is the maximum value of X, and Xi is the normalized data. Thus, the inputs and outputs are scaled between ŌłÆ1 and 1.
Artificial neural networks are developed based on the neurons of the human brain and are widely used in different fields. They can be employed to predict the nonlinear behavior of various variables. A typical neural network consists of an input layer, a hidden layer, and an output layer. Each layer contains some neurons or nodes, and each neuron is connected to other neurons. The number of neurons in the input layer is the same as the number of input variables and the number of outputs also defines the number of neurons in the output layer. However, the number of neurons and layers in the hidden layer are designed based on the complexity of the problem. One of the well-known types of artificial neural networks, which is also used in this study, is feedforward neural networks or multi-layer perceptron (MLP). In these types of neural networks, all the existing neurons in one layer are fully connected to the neurons of the next layer and pass the data in a forward direction through the network by using certain weights and biases [35]. A back propagation training algorithm is used to transfer the errors to previous layers to adjust the weights and biases and minimize the errors between the predicted output and the desired output (target). The concept of these structures was developed by Rumelhart et al. [36] and could be expressed as follows:
where y is the output of the neural network, x is the input, wi are the weights, and b is the bias [37,38].
The MLP structure for a specific case is shown in Fig. 4. In this study, MATLABTM is used to design a feedforward neural network. The first layer of this MLP model is the input layer with five nodes. Three hidden layers are used with different number of neurons in each of the layer. The output layer has only one neuron since this model has only one output which is spread ratio in one case and Shinokura coefficient in the other case. The prediction of the spread for oval and round caliber are done by separate MLPs and for each case two MLP model is used with the same inputs but different outputs. Thus, MLP-1 and MLP-2 are designed to predict the spread in oval caliber, MLP-3 and MLP-4 are used to predict the spread in round caliber. The input layer for all MLPs has 5 input variables which are rolling velocity (with a unit) and dimensionless values of friction, geometry, backward and forward tension. The output for two MLPs is the spread ratio (Sr) and for the other two MLPs, the output is the ╬▒ coefficient of ShinokuraŌĆÖs equation which are both dimensionless values. The inputs and outputs of all MLPs are shown in Table 7.
The number of hidden layers and neurons for all MLPs which are found based on the grid search is three hidden layers. The transfer function of all layers is ŌĆ£TANSIGŌĆØ except the output layer which is ŌĆ£PURELINŌĆØ. ŌĆ£TRAINLMŌĆØ function which is based on the Levenberg-Marquardt optimization is used as the training method to adjust weights and biases. Since each input parameter is changed 5 or 6 levels and the total number of data set is limited, the random data division may result in a biased test data set. Thus, manual data division is used to ensure that the validation and test sets demonstrate good representatives of the whole data set.
The default and used parameters for MLPs are shown in Table 8. In addition, the root mean square error (RMSE) and correlation coefficient (R) are used to evaluate the predicted values (outputs) with respect to the data from simulations (targets) in a form of linear regression analysis.
In this way, four MLPs are used to predict the spread in oval and round calibers of wire rod rolling. The output of MLP-2 and MLP-4 can be converted to spread ratio by using Equation 2 and reverse calculation. Therefore, the output of MLP-1 and MLP-2 are the same and can be fused together.
Fuzzy logic, which was introduced by Zadeh in 1965 [39], provides the possibility of utilizing vague or uncertain data based on IF-THEN rules to make decisions. Jang proposed an intelligent hybrid system, ANFIS, in 1993 which takes the advantage of artificial neural networks and fuzzy logic simultaneously [40]. ANFIS is based on the fuzzy if-then rules of the Takagi-Sugeno (T-S) fuzzy inference system [40,41] and can be used for modeling complex systems with nonlinear relationships between inputs and outputs by using the adaptive learning of neural network and the human-like reasoning method of fuzzy systems [40]. In addition, fuzzy rules are added to the neural networks that help to increase the reasoning and explainability of the model in comparison with the artificial neural networks which are considered a black box approach since it is difficult to find how they work after the training process [42,43].
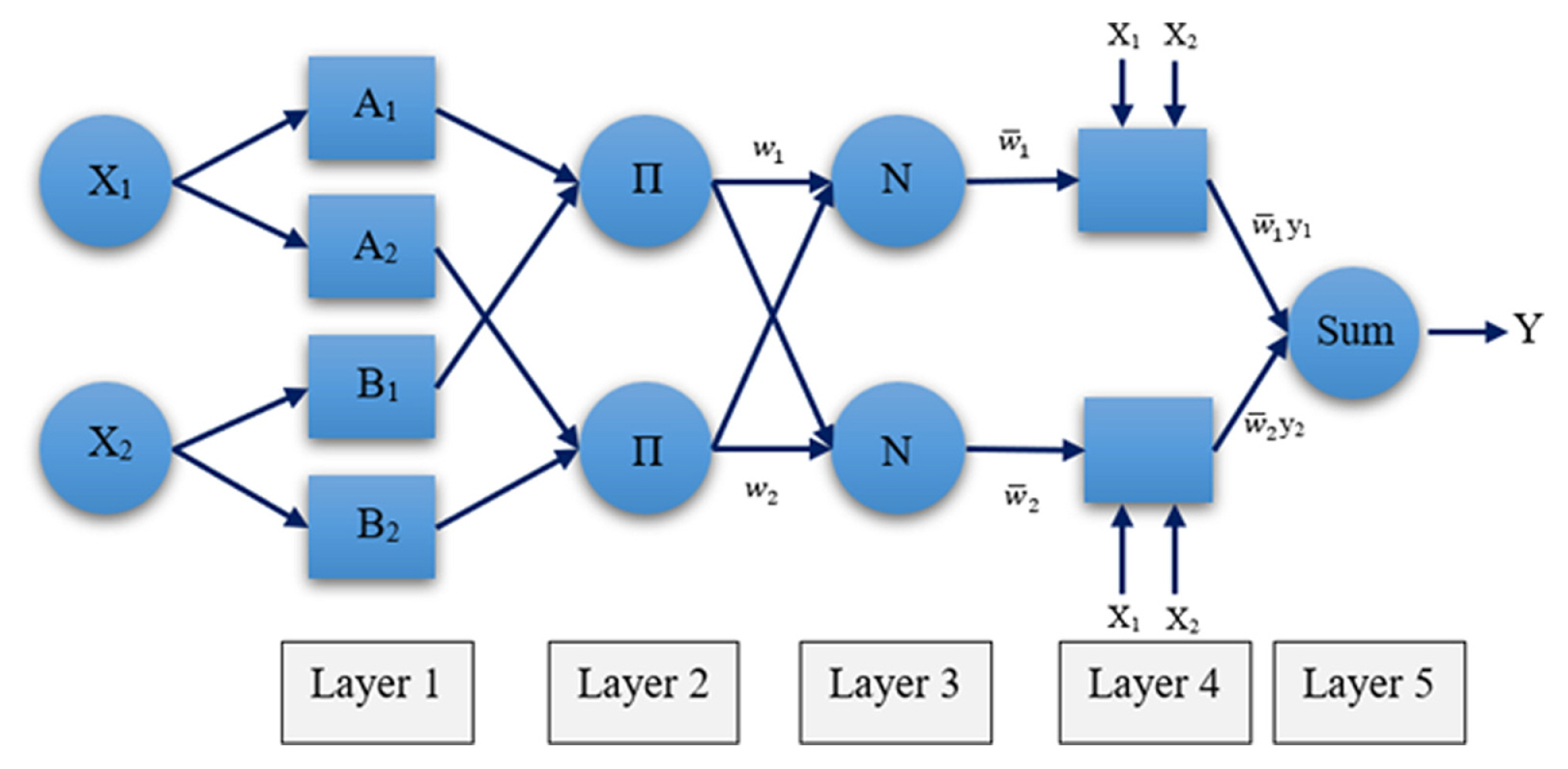
For the sake of simplicity, an ANFIS structure of the T-S type with two inputs, one output (Y), and five layers is demonstrated in Fig. 5. The rules of this system can be represented as:
where X1 and X2 are the inputs, Ai and Bi are fuzzy sets, yi is the variable of consequence, pi, qi, and ri are the consequence parameters of the T-S model [41]. In the first layer, the membership functions are generated so the inputs are fuzzified. Each node in this layer is an adaptive node with a node function as follows:
where ╬╝Ai (X1) is the membership degree of X1 in the fuzzy set of A and Oi1 is the output of the node in the ith position in the first layer. The Gaussian membership function used in this study with the following equation:
where x is a variable, Žā and c are premise parameters. In the second layer, the strength of each rule (wi) is calculated by multiplying all inputs of a node and then is normalized considering the firing strength of all rules (w╠äi) in the third layer.
In the fourth layer, a first-order linear equation is used to calculate the values of the consequences of each rule and the summation of all of them is the final output in the fifth layer with the following equations:
The input and output variables are the same as what was used for MLP (Table 7). In this step, two ANFIS models (ANFIS-1 and ANFIS-2) are designed to predict the material spread of oval caliber and the other 2 models (ANFIS-3 and ANFIS-4) are considered to predict the material spread of round caliber in wire rod rolling. Gaussian type is used for all the membership functions (MFs) and the number of MFs is determined based on trial and error.
The best result is obtained with four MFs and 100 epochs with the particle swarm optimization (PSO) learning for the ANFIS structure. In addition, fuzzy c-means clustering is used in the structure of ANFIS which classifies the inputs into similar groups. By using this method, the number of rules is decreased in comparison with the grid partitioning. All the parameters used to design the ANFIS are shown in Table 9.
In this way, four ANFIS models are designed and used to predict the spread in oval and round calibers of wire rod rolling. The same as the MLP models, ANFIS-1 and ANFIS-2 are used for the oval caliber and the result of them can be converted to spread ratio by using Equation 2. ANFIS-3 and ANFIS-4 are also used for the round caliber and the outputs can be changed to spread ratio with the same strategy.
The data fusion process takes the outputs of all MLP and ANFIS models and combines them to provide a single output. The idea behind using a fusion step is to increase the consistency and accuracy of the prediction model. Since different sub-models may have errors in the prediction of some cases, combining the output can decrease the errors and increase the robustness of the model. In the proposed spread prediction model, the fusion of all data is used to predict of spread for those new cases that are out of the range of simulations. Two MLP models and two ANFIS models are designed to predict the spread ratio and ╬▒ coefficient for each type of caliber. By using the Shinokura equation, the obtained ╬▒ coefficient can be converted to the spread ratio by reverse calculation. Therefore, the result of all MLP and ANFIS models will be the spread ratio which can be used for data fusion.
An unweighted average is used to combine all the inputs of the fusion process to provide a single output for the prediction model. The output of the fusion step is the spread ratio which is then converted to spread by multiplying the initial width of the material. Finally, the obtained spread is added to the initial width of the material, so the maximum width of the material will be obtained after the rolling process. The structure and steps of the model are shown in Fig. 6.
Eight models based on MLP and ANFIS are designed to predict the spread in oval and round caliber which means for each caliber four models are considered. The models are trained and examined separately based on the obtained data from the FE analysis. The fusion process is employed when the trained models are used to predict the spread based on the new data which have not been seen by the trained models in training, validation, and test data sets. By using ShinokuraŌĆÖs model and reverse calculation, the output of all models becomes similar, so an unweighted average is used to provide a single output. Since the errors can be decreased by the summation of all models, the robustness and accuracy of the model increase by using the fusion step when it is used in real applications.
The obtained data from a steelmaking company is used for the verification of the FE analysis. When it is verified, the same conditions are used to do other simulations and generate data for the training purpose. Based on the factory data, a six-stand rolling is used for the verification of FE analysis. The input and output areas of the material passed through six-stand rolling are obtained from the existing sensors in the factory and then compared with the output area of the simulations. Based on the verified model, other simulations are done, and the results are investigated to determine the important parameters that have a significant effect on the spread ratio in steel wire rod rolling. In the next step, the results of input parameters that do not have a significant effect on the spread ratio are removed from the input database and the remaining inputs are changed to dimensionless values. By using MLP and ANFIS, an accurate mapping of inputs to the output is achieved for all models.
Based on the obtained data from the steelmaking company, the area of the material cross-section in specific sections is measured by using the sensors. The input and output sections are shown in Fig. 7(a). To verify the FE analysis, all the processing conditions such as temperature, rollers rotational speed, rollers diameter, caliber type and dimensions, roll gaps, steel grade, and friction for all rolling stands are selected the same as the real conditions in the factory. The model that has been used for the FE analysis is shown in Fig. 7(b).
The input and output cross-sectional areas obtained from the factory are 866.6, 225.6 mm2, respectively. The position of the input cross-section is before the first stand of rolling and the position of the output cross-section is after the sixth stand of rolling which is shown in Fig. 7(a). The same input area is used for the simulation and the area of the output cross-section obtained from the FE analysis by ABAQUSTM is 229.08 mm2 which shows a 1.5% deviation from the experimental values. It is also worth mentioning that there may be some errors in the measurements and the values from the factory may be a little different from the real values. However, the simulated results are perfectly matched with the real data which shows the employed ABAQUSTM model is correct and can be used for the rest of the simulations and case studies.
As is shown in Equation 2, some parameters such as friction and tension are not considered in ShinokuraŌĆÖs equation. Even though it is based on several experiments and the effect of friction may be considered indirectly, there is not a clear understanding and control over these parameters when they are used in practical applications. By simulating different cases, it is possible to understand the effect of each parameter. The results of simulations where ShinokuraŌĆÖs model does not consider these input variables on the spread ratio are shown in Fig. 8. Friction is one of the most important and complex factors that affects the spread ratio. In the rolling of bars and small-width slabs, the increase in friction lead to an increase in the spread ratio since friction normally causes lower material flow in the longest direction [44,45]. As is shown in Fig. 8(a), when the friction increases, the spread ratio increases as well, which is in line with previous studies [44,45].
The rolling rotational speed also affects the spread ratio at low speed; however, its effect becomes negligible at higher speeds (Fig. 8(b) ). Temperature and material strength, on the other hand, have a very small effect on the spread ratio over a wide range of changes which is not considered a decisive parameter in this study (Figs. 8(c) and 8(d)). These findings are also in line with the previous studies [3,33].
The other results of FE analysis and the ShinokuraŌĆÖs model with ╬▒ factors of 0.83 and 0.97 are shown in Fig. 9 in which the roll gap, the input material size, and the roller diameter are changed. ShinokuraŌĆÖs model can approximately predict the spread when the geometrical parameters are changed. Thus, it approximately has a similar trend to the result of FE analysis, however, there is a vertical shift when different ╬▒ factors are used. If the correct ╬▒ factor is selected, it can predict the spread ratio with good accuracy. The problem is the lack of a standard approach for finding the correct ╬▒ factor.
Interstand tension is one of the most important variables that can affect the spread ratio. Changing the rotational speed of the rollers and using a looper can result in changing the tension between the rolling stands. In this study, a three-stand rolling is considered to study the effect of interstand tension on the spread ratio. If the speed of these three rollers is changed, the tension between the stands, which is a longitudinal force, will be changed. This force can cause a push or pull action in the material and change the spread of rolled material.
For a three-stand rolling, backward and forward tensions are defined (Fig. 2). When considering the second roller, the backward tension is defined as the tension that exists between the first and the second roller or the tension on the entry side of the second roller. The forward tension (for the second roller) is also defined as the tension that exists between the second and third roller or the tension at the exit side of the second roller. In addition, the forward tension in one stand is also the backward tension for the next stand, and the interstand tension is considered positive when it is tensile in which the material experiences a pulling force [45].
The backward tension is a function of the rotational speed of the first and second roller, therefore, any changes in these speeds will change the interstand tension. To understand the effect of backward tension, the rotational speed of the first roller is changed at five levels while the speed of the other rollers is kept constant. An increase in the speed of the first roller results in the reduction of the backward tension which means the material (between the first and second roller) experiences a lower tension or a pulling force. Thus, the material tends to have higher width after the first stand of rolling. Since the material at the entry section of the second roller has higher width, the width of the material after the second roller increases which is shown in Fig. 10(a). For the forward tension, the speed of the third roller is changed while the speeds of other rollers are kept constant. Therefore, an increase in the speed of the third roller results in an increase in the forward tension which means the material between the second and third roller experiences a higher pulling force. Thus, the material tends to have lower width after the second stand of rolling which is shown in Fig. 10(b). Based on the previous studies, the effect of backward tension should be higher than the forward tension [45] which is also in line with the current results. However, ShinokuraŌĆÖs model shows errors in the prediction of the spread ratio while the interstand tension is changed.
Based on the simulations of one-stand rolling and three-stand rolling, it is understood that ShinokuraŌĆÖs model results in large errors for the prediction of the spread ratio when the processing parameters are changed. It can predict the spread ratio when the geometrical parameters are changed, however, selecting the correct ╬▒ coefficient is a challenge in these cases. Based on the effect of input parameters on the spread ratio, the geometrical parameters, speed, friction, and interstand tensions are used for the training, the temperature and material strength are not considered due to their small effects on the spread ratio. For the output parameter, the spread ratio and the ╬▒ coefficient of ShinokuraŌĆÖs model are considered which can be changed to the spread and width of the material after rolling.
The spread ratio and ╬▒ coefficient in oval and round calibers are predicted by using separate MLP models with the hyperparameters shown in Table 8. The training, validation, and test data are selected manually, thus, each set of data has representatives in the test data set which provides a better evaluation of the MLP models performance.
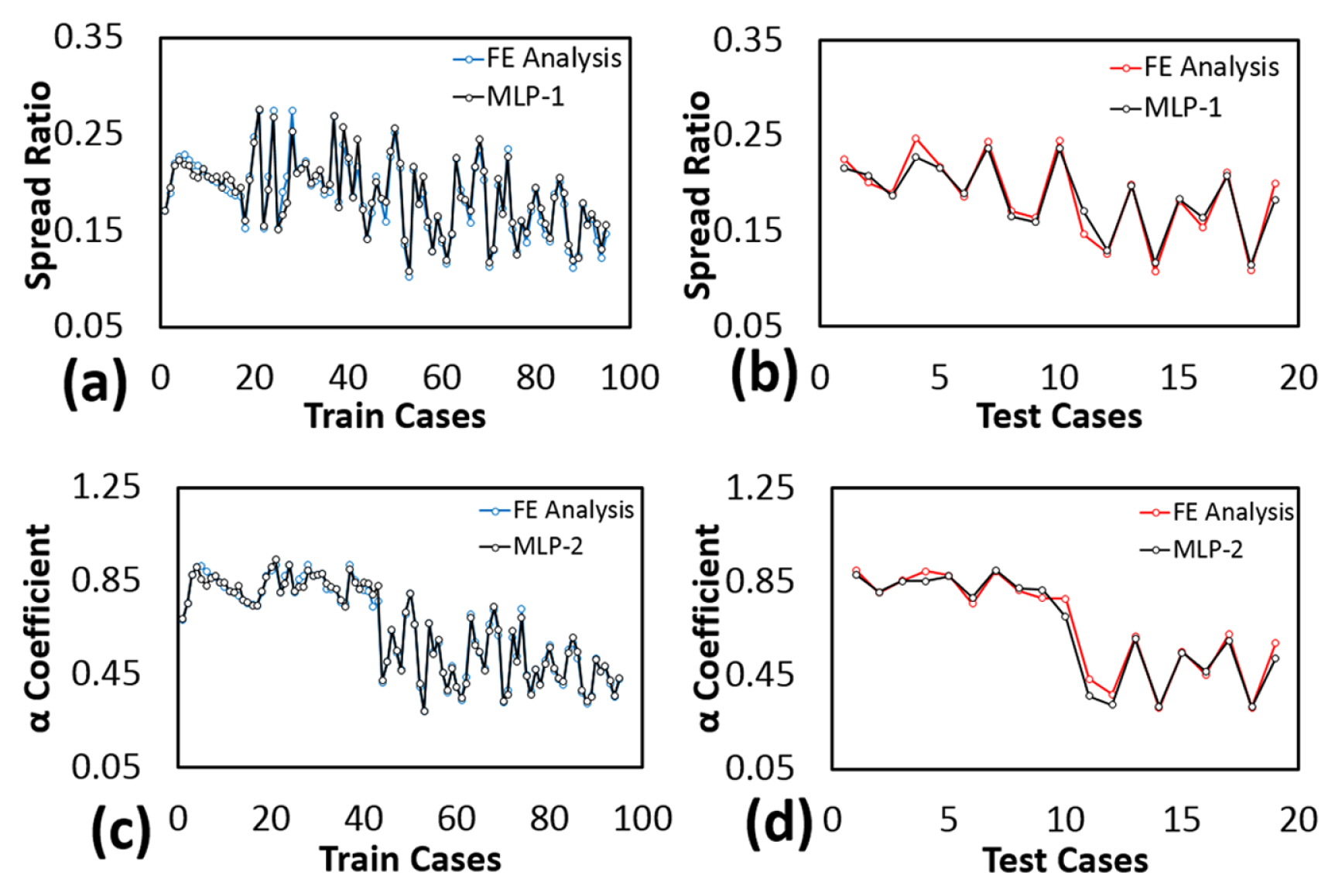
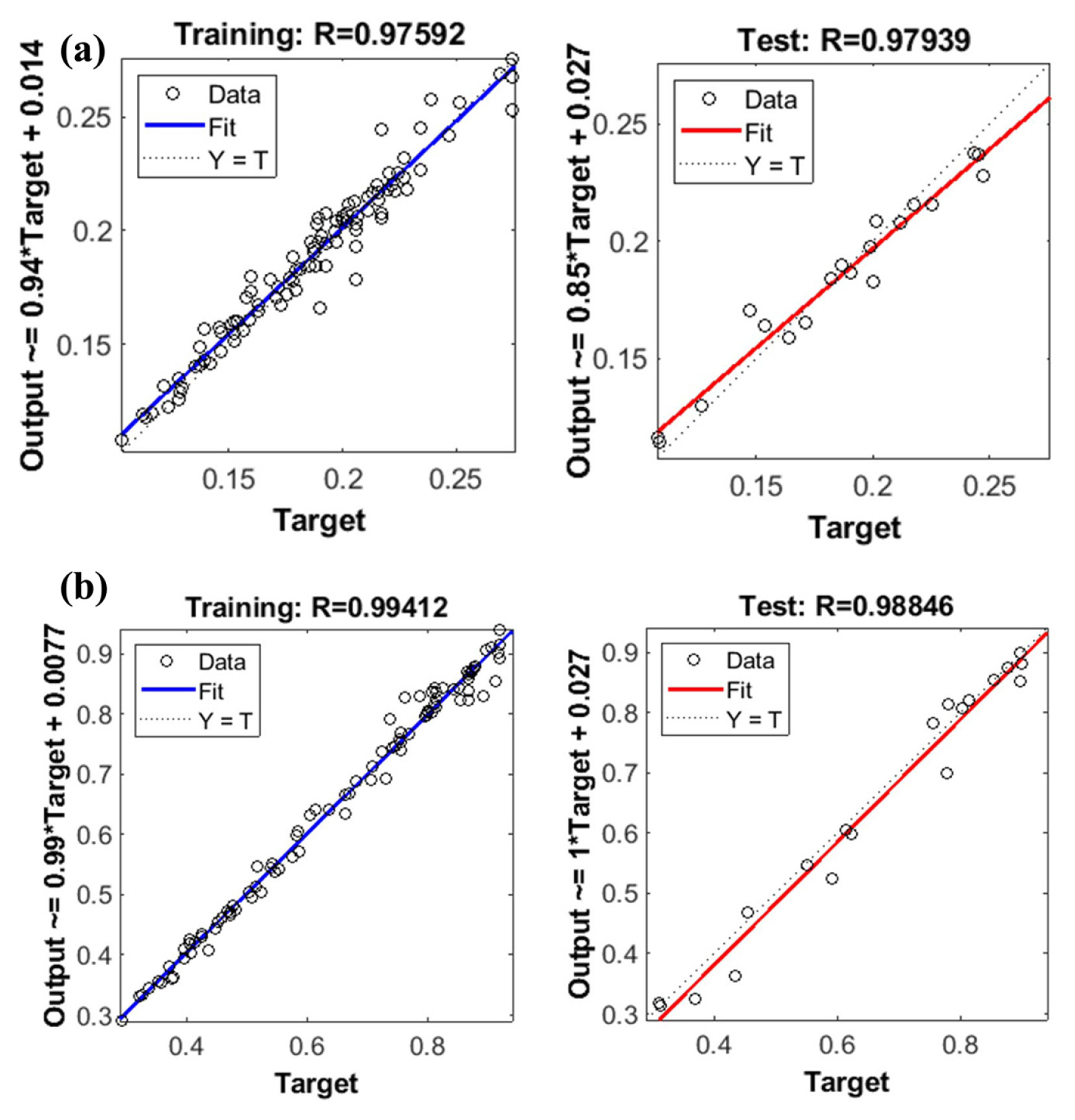
The FE analysis results and the predicted values of spread ratio and ╬▒ coefficient by MLP models for oval caliber (MLP-1 and MLP-2) are compared in Fig. 11. Furthermore, the performance of the MLP-1 and MLP-2 are shown in Fig. 12.
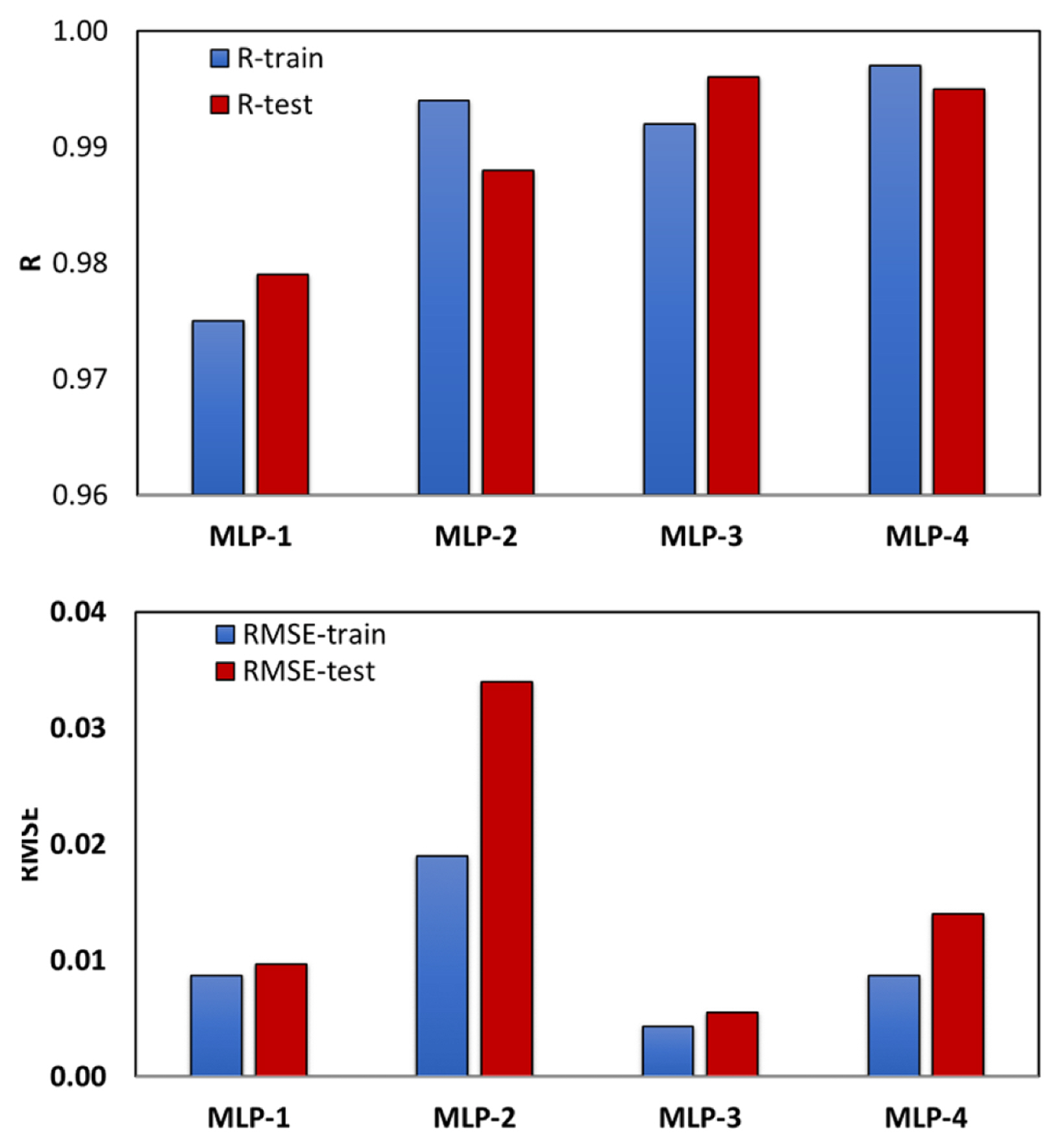
The correlation coefficients (R) for training and test data are 0.975 and 0.979 for MLP-1 and 0.994 and 0.988 for MLP-2, respectively. In addition, the RMSE for test data of MLP-1 and MLP-2 is 0.009 and 0.034, respectively.
The same as the oval caliber, the results of MLP models (MLP-3 and MLP-4) for round caliber are obtained. The correlation coefficients (R) for training and test data are 0.992 and 0.996 for MLP-3 and 0.997 and 0.995 for MLP-4, respectively. In addition, the RMSE of test data sets for MLP-3 and MLP-4 is 0.005 and 0.014, respectively. Finally, the comparison between R and RMSE of train and test data is shown in Fig. 13. MLP-2 shows the highest RMSE values in comparison with other models. However, that would be better to compare the RMSE of those MLPs with the same output since the values of ╬▒ coefficients are normally higher than the values of the spread ratio. Finally, it can be inferred that the trained MLP models can predict the spread in wire rod rolling with good accuracy.
For the ANFIS section, fuzzy c-means clustering is used instead of the grid partitioning in the structure of ANFIS which decreases the number of rules and the training time.
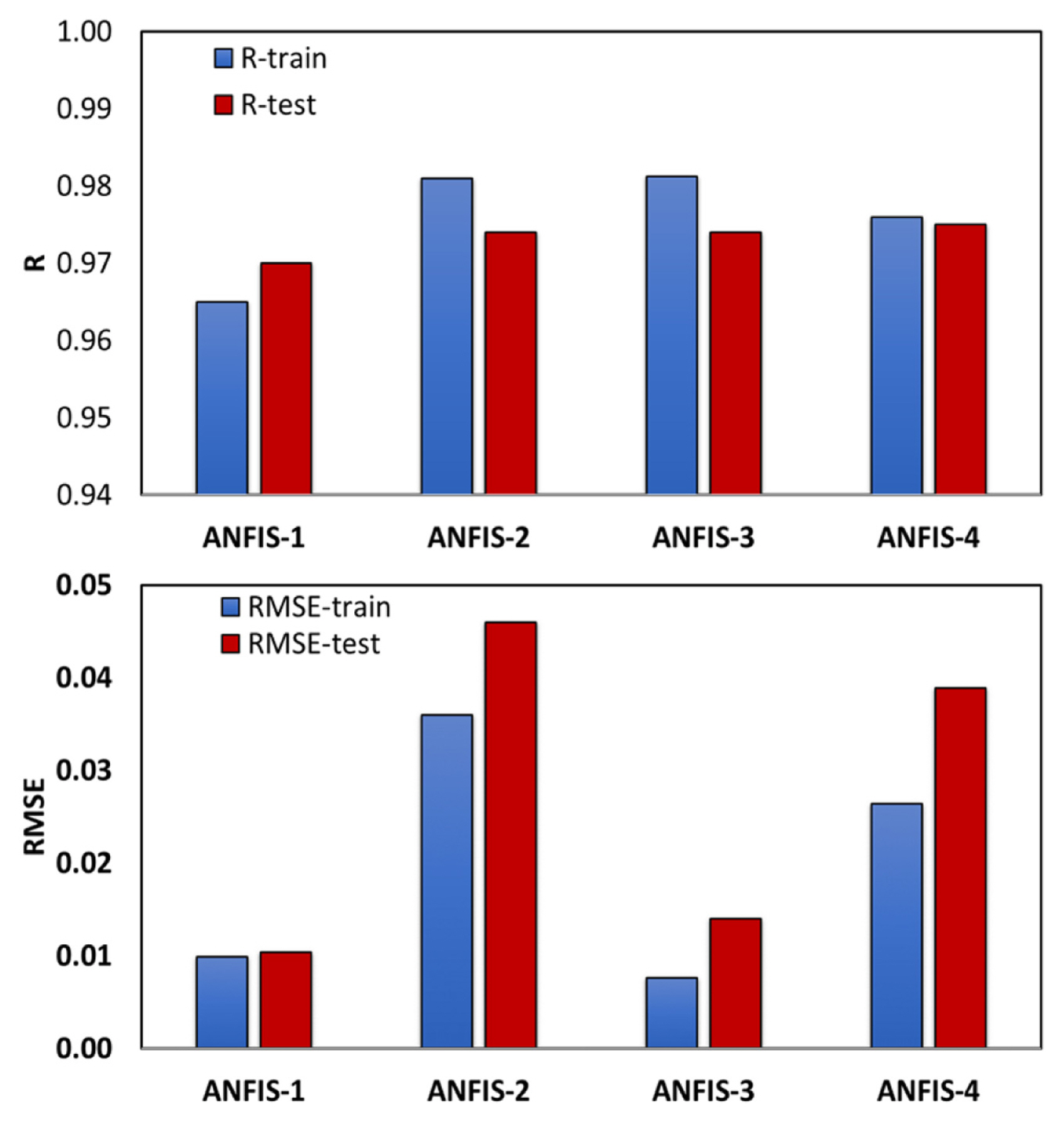
The best results were achieved by using four clusters/rules for all the ANFIS models. The result of ANFIS models for oval caliber (ANFIS-1 and ANIS-2) are shown in Fig. 14. The correlation coeff icients for training and test data are 0.965 and 0.9708 for ANFIS-1 and 0.981, 0.9740 for ANFIS-2, respectively. The prediction results of ANFIS models for the round caliber (ANFIS-3 and ANFIS-4) are also obtained with the same approach. The correlation coefficients for training and test data are 0.981 and 0.9745 for ANFIS-3 and 0.974, 0.975 for ANFIS-4, respectively.
The comparison between R and RMSE of train and test data for ANFIS models is shown in Fig. 15. Since the values of the spread ratio are lower than the ╬▒ coefficient, the RMSE of ANFIS-2 and ANFIS-4 are higher than the other two ANFIS models which is related to the prediction of the spread ratio. The results demonstrate that ANFIS can be used to predict spread in steel wire rod rolling, however, the result of MLP models shows higher accuracy in comparison to ANFIS models.
Transferability is one of the most important aspects of AI-based approaches in practical applications. Most models are trained based on specific data sets obtained from experiments, simulations, and so on. By using different algorithms and finding the optimal hyper-parameters, it is possible to achieve acceptable accuracy in the test data sets. However, one of the challenging parts of these models is the transferring process from the controlled simulation environment to the practical applications where new data sets have not been examined by the trained models. In addition, it is of interest to obtain information from the AI models which demonstrate how input parameters can affect the output and which parameters have the highest and lowest effects on the output. By using the ANFIS models, some level of reasoning can be achieved which will increase the explainability of the prediction system.
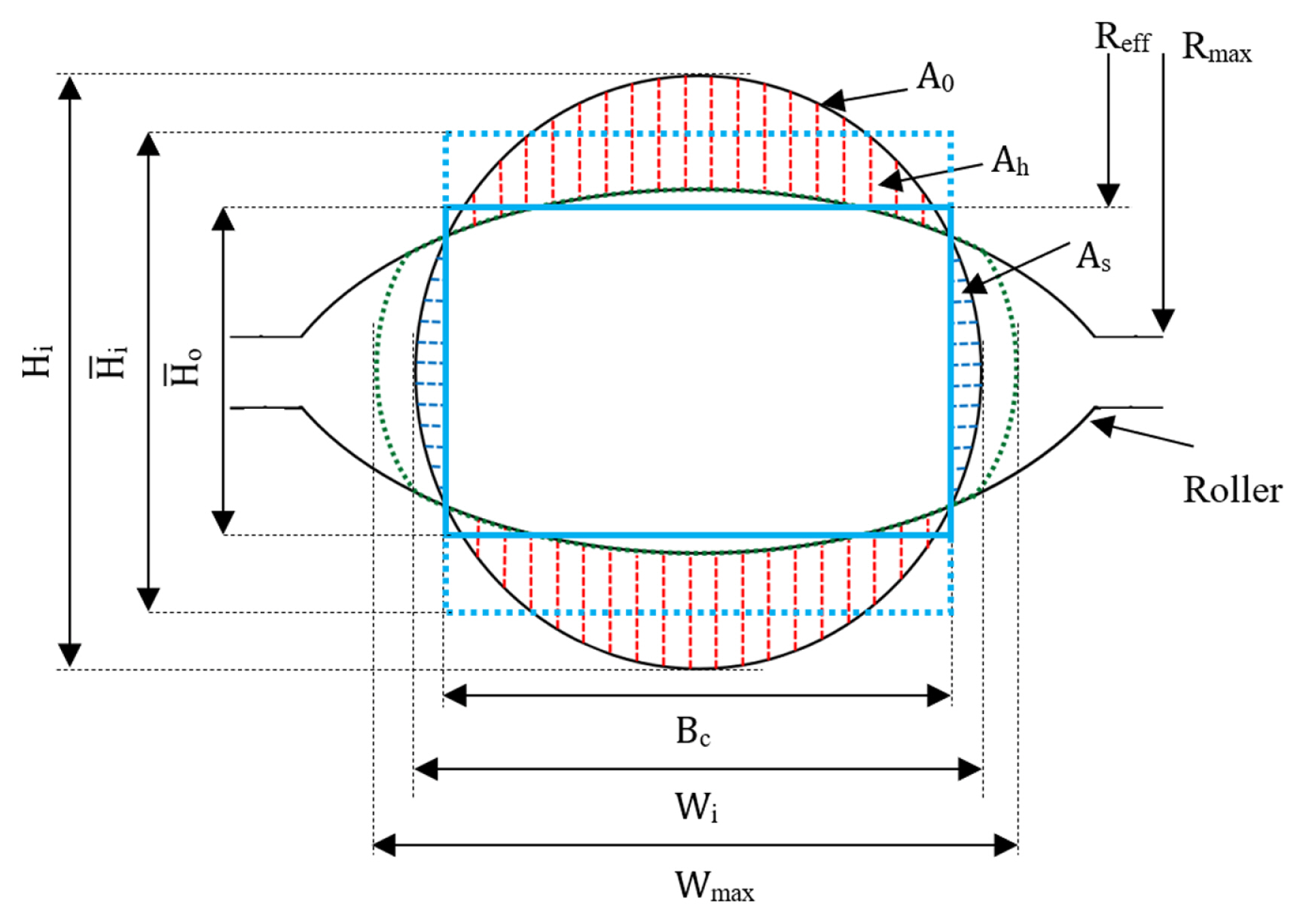
To have a better view of the effect of different input parameters, two other ANFIS models are used with the same hyper-parameters shown in Table 9. The inputs of these models are friction, speed, roll diameter, speed, H̄o, backward and forward tension, and the output is also the maximum width after the rolling process. Based on Fig. 3, H̄o is considered as the input instead of the roll gap since the effect of both the roll gap and roll groove radius is included in this parameter. Thus, it can represent the effect of both parameters on the output.
A reference condition is considered in the three-stand rolling and only one variable in each graph is changed from its minimum value up to its maximum value while other variables are kept constant, thus, the relative effect of each input parameter on the output can be understood.
This calculation is done for all input parameters and the final output width is normalized to the range of 0 to 1 as well as each input variable. The normalized graphs are then plotted, and a linear regression is done for all curves. The slope of the normalized curves is considered as the relative effect of each input parameter which is shown in Fig. 16. The results demonstrate that the backward tension and roll diameter have the highest effect, and the rotational speed of the roller has the lowest effect on the material width in the steel wire rod rolling process. It is worth mentioning that the temperature and material strength were previously removed from the input variables due to their low effect on the output. These results of ANFIS explain the effect of different input parameters on the output and can be used in practical applications to adjust the input parameters to have the desired output width. In addition, a relationship that exist between the input and output parameters of the data set can be extracted as a rule by the model which provides some level of reasoning for the user.
The results of ANFIS models are also shown as colormaps in Fig. 17 which represents the effect of two input variables on the output width.
To obtain the colormaps, the same reference condition is considered and the other two variables in each graph are increased from their minimum values up to their maximum values. As explained in the FE analysis result section, by increasing the roll diameter and friction the output width increases and by increasing the speed, roll gap (or H̄o ), backward and forward tension the output width decreases. The results of the ANFIS model are also in line with the FE analysis results which show the ANFIS model can understand the correct effect of different input parameters on the output and provide these relationships for the user.
The proposed AI model is trained based on a specific range of geometries, however, different input material sizes and several calibers with various geometries are used under different processing conditions in the production of the steel wire rods. Due to the existence of many possible cases, it is not an efficient method to do FE analysis for all possible cases and then use them for training of the model. Thus, the FE analysis is done within a specific range and then dimensionless values and fusion of all the models are used to transfer the trained model from a specific domain to other setups of the wire rod rolling. Therefore, the obtained dimensionless values do not belong to specific dimensions and processing conditions. Furthermore, since four AI models are used for each type of caliber, the fusion of all these models can increase the accuracy and reliability of the model.
Based on the obtained experimental data from the steelmaking company, the verification of the FE analysis was done by using a six-stand rolling model. The same model is also used for the verification of the transferability of the proposed model. The input material for the FE analysis was a circular cross-section with a diameter of around 73 mm; however, the input material for the six-stand rolling is a circular cross-section with a diameter of around 20 mm. In addition, the roll gap, size of caliber, rolling speed, and other parameters are different from the initial case that was used for the training of the models. Therefore, this can be considered a good case to examine the transferability aspect of the proposed AI-based method. The schematic view of the six-stand rolling model with the sections used for measurement is shown in Fig. 18(a). The section between each stand is used to measure the width of the material and then it is compared to the result of the prediction model (Fig. 18(b)). For the prediction of width in each oval and round caliber, four models are used in which MLP-1, MLP-2, ANFIS-1, and ANFIS-2 are used for oval caliber and MLP-3, MLP-4, ANFIS-3, and ANFIS-4 are used for the round caliber. Then, an unweighted average is used to sum all the outputs of four models to provide a single output. The result of each model, the fusion, and the error calculated with respect to the reference condition are shown in Table 10. The lowest and highest errors for each section are 0.26% and ŌłÆ1.3% which shows the high accuracy and transferability of the proposed model.
Therefore, the proposed model by employing dimensionless data and data fusion can predict the width of material in the steel wire rod rolling process with high accuracy. Due to the using several AI models, the possibility of error decreases and the reliability of the model increases. In addition, the use of ANFIS provides some level of reasoning and explains how the model predicts the width by demonstrating the effect of each input parameter on the output. Finally, the proposed model shows that it can be transferred to other setups where the dimensions and processing conditions are completely different from what was used in the training section.
There are some limitations and assumptions associated with this study. The number of FE analyses is limited to around 300 cases due to the long FE simulation time of 3D wire rod rolling (especially for the three-stand rolling). In addition, it is desired to perform additional FE analysis with more steel grades to elucidate the effect of different steel grades on the spread even though the strength of the material is changed over a wide range. Finally, the number of sensors to obtain the actual cross-sectional area of the rolled material is limited to a few stands in the factory which is a limitation to obtaining data about the cross-sectional area after all stands of rolling and using them for further examination of the model.
In this study, a method is proposed to predict the spread in the steel wire rod rolling process which is based on the results of FE analysis and employing multiple AI methods. The current AI-based approach is developed to overcome the low accuracy and generality of the available empirical models.
Based on the FE analysis, it is understood that friction, speed, backward tension, forward tension, roller diameter, roll gap, and input material size are the important parameters affecting the spread in the steel wire rod rolling process. For each type of caliber, four models including MLP and ANIFS are separately trained to predict the spread based on the result of FE analysis. The lowest and highest correlation parameters (R) among all models were 0.9708 for ANFIS-1 and 0.996 for MLP-3, respectively. The lowest and highest RMSE were also 0.009 for MLP-1 and 0.055 for ANFIS-4, respectively. Due to the use of data fusion for the prediction of new data sets and the dimensionless values for all inputs and outputs, the proposed model is independent of dimensions and processing conditions which makes the model transferable. In addition, the data fusion combines the output of all AI models and provides a single output which increases the accuracy and robustness of the model. Due to the use of ANFIS, it is understood that the most effective input parameters in the wire rod rolling process are roller diameter and backward tension while the rotational speed of the roller is the least important parameter. In addition, the effect of each input parameter on the output is understood which increases the level of reasoning of the model. The transferability of the proposed model was verified by using a six-stand rolling which was not previously used in the training and test data sets. The model could successfully predict the width of material in five sections and the predicted results were in good agreement with the measured values.
Fig.┬Ā4The structure of MLP-3 and MLP-4 used for prediction of spread ratio and Shinokura coefficient 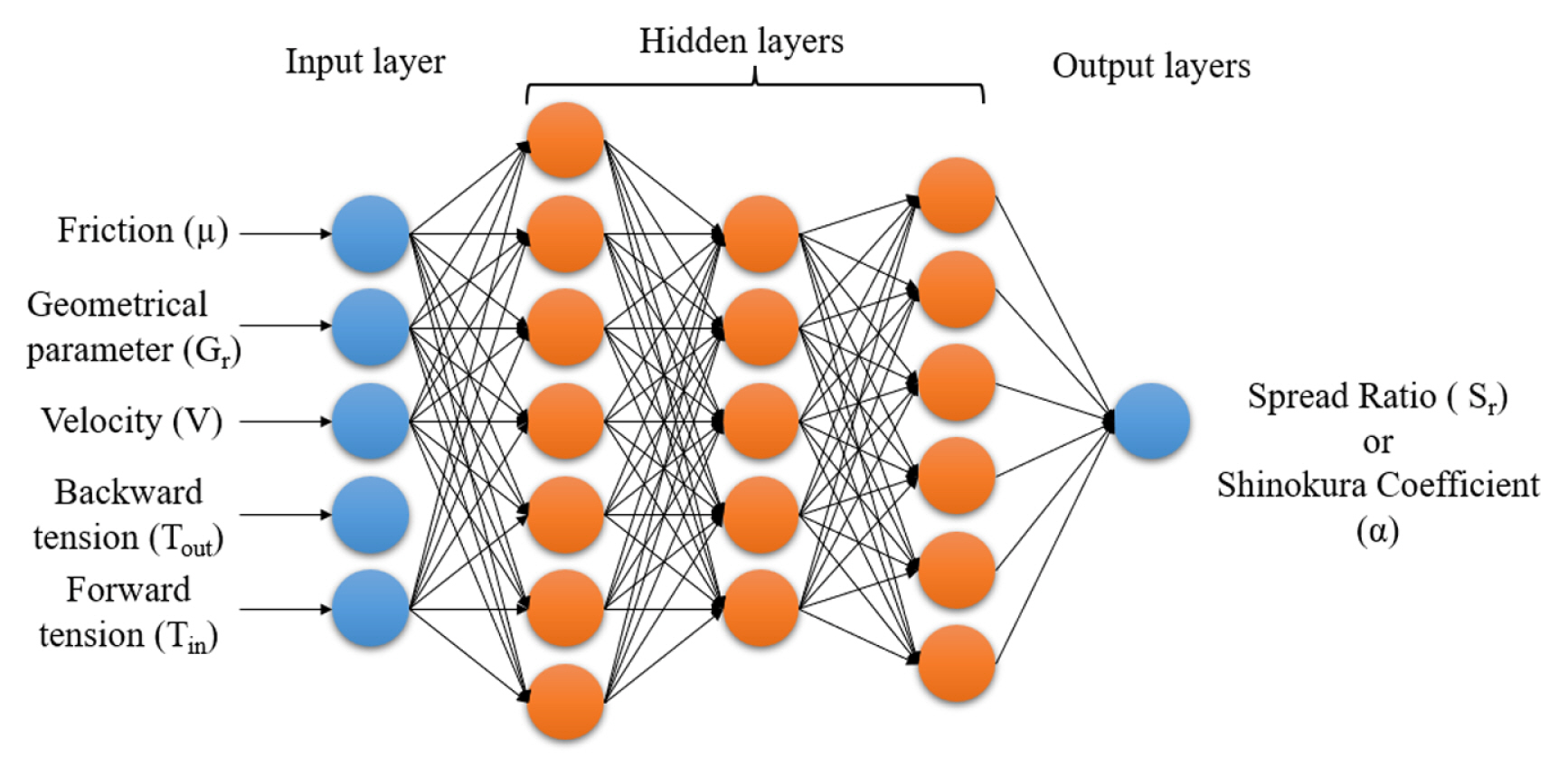
Fig.┬Ā7(a) Positions of the sensors to obtain input and output cross-sectional area in the steelmaking company and (b) The model used to simulate the six-stand rolling for the verification 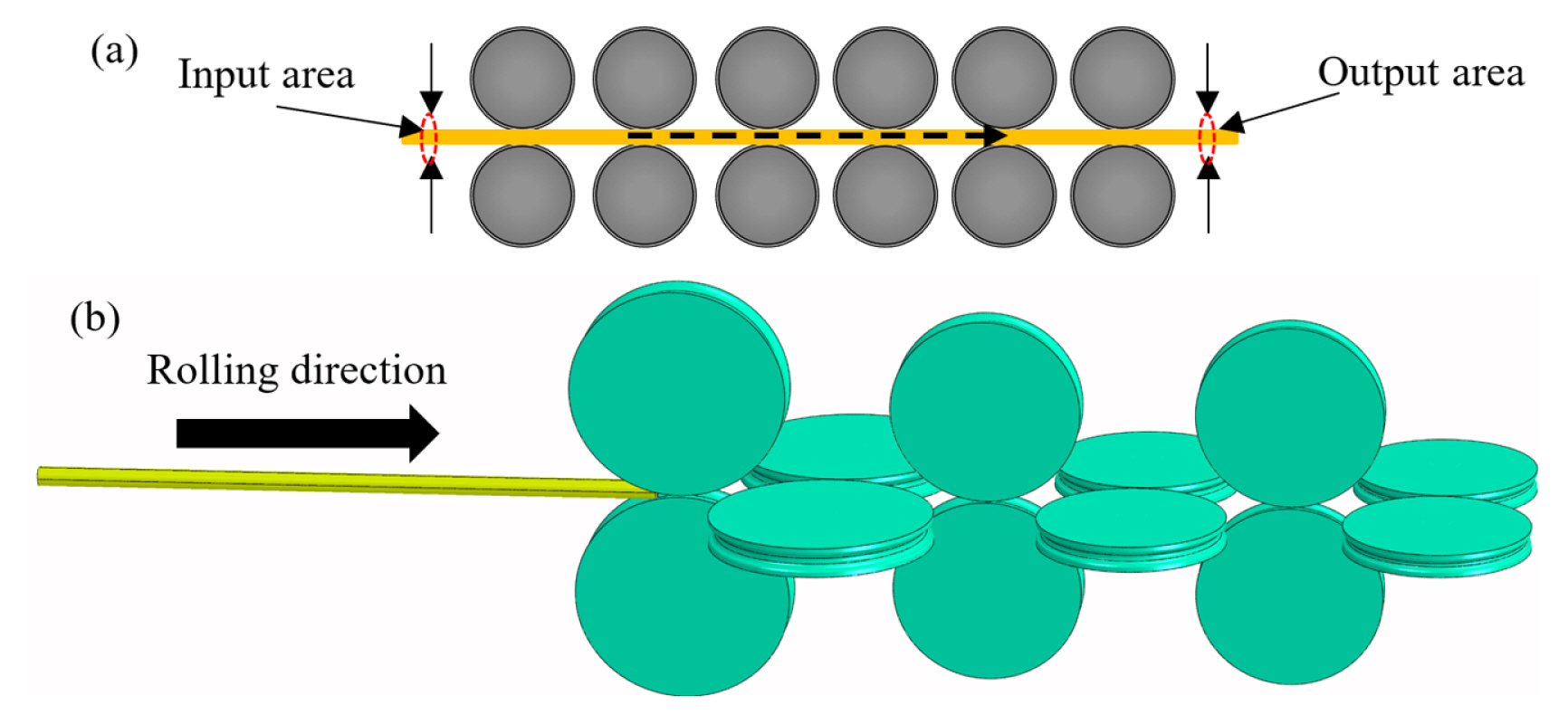
Fig.┬Ā8The effect of (a) Friction, (b) Roller rotational speed, (c) Material strength, and (d) Temperature on the spread ratio in one-stand rolling of oval caliber 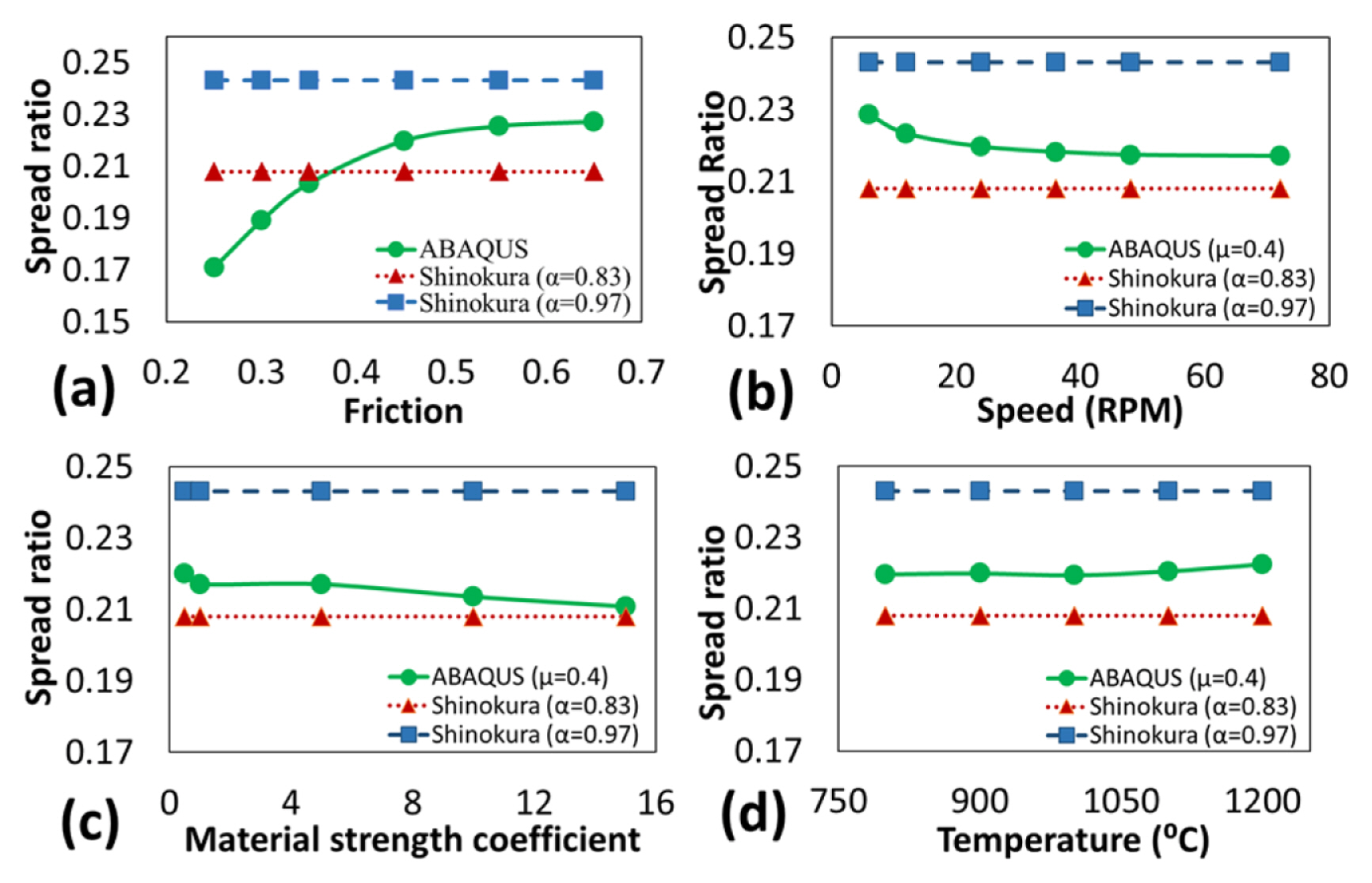
Fig.┬Ā9The effect of (a) Roll gap, (b) Material size, and (c) Roller diameter on the spread ratio in one-stand rolling of oval caliber 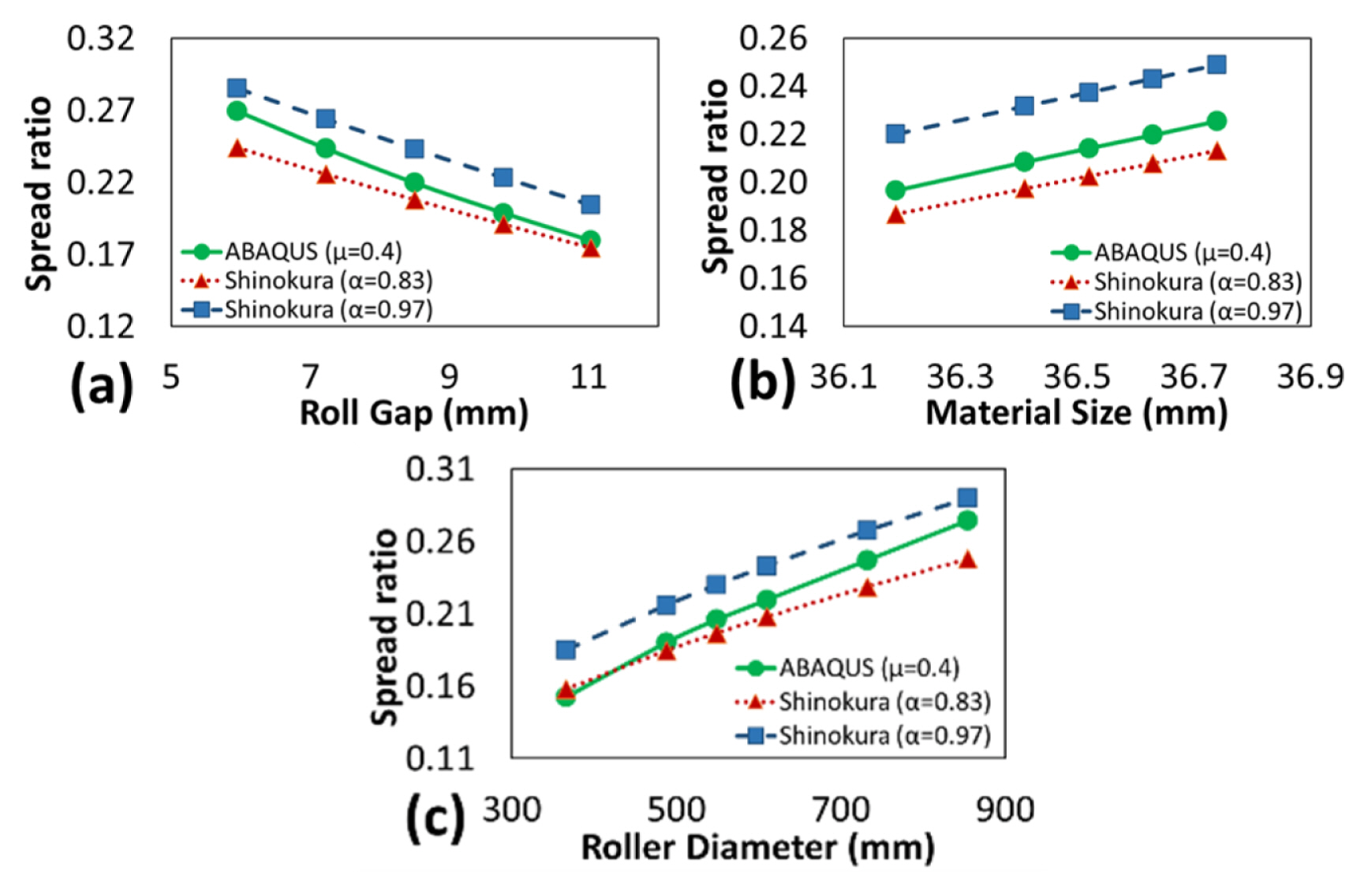
Fig.┬Ā10The effect of (a) Backward tension and (b) Forward tension on the spread ratio in three-stand rolling of the round-oval-round caliber 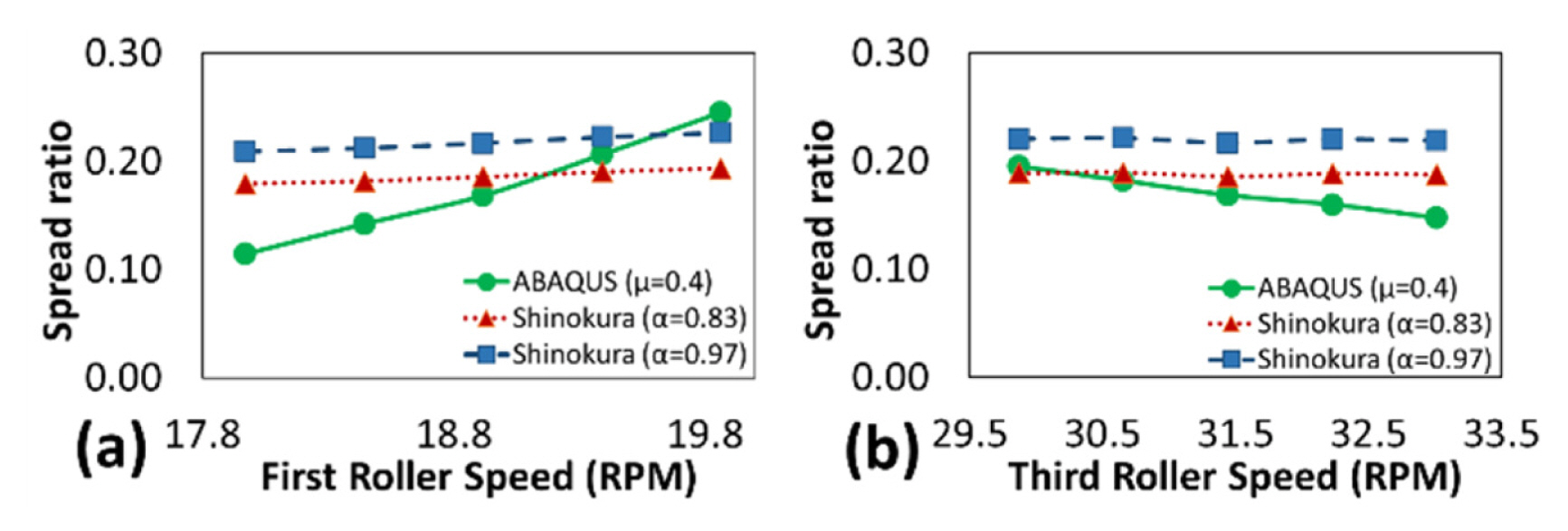
Fig.┬Ā14Comparison between the result of (a), (b) ANFIS-1 and (c), (d) ANFIS-2 with their FE analysis 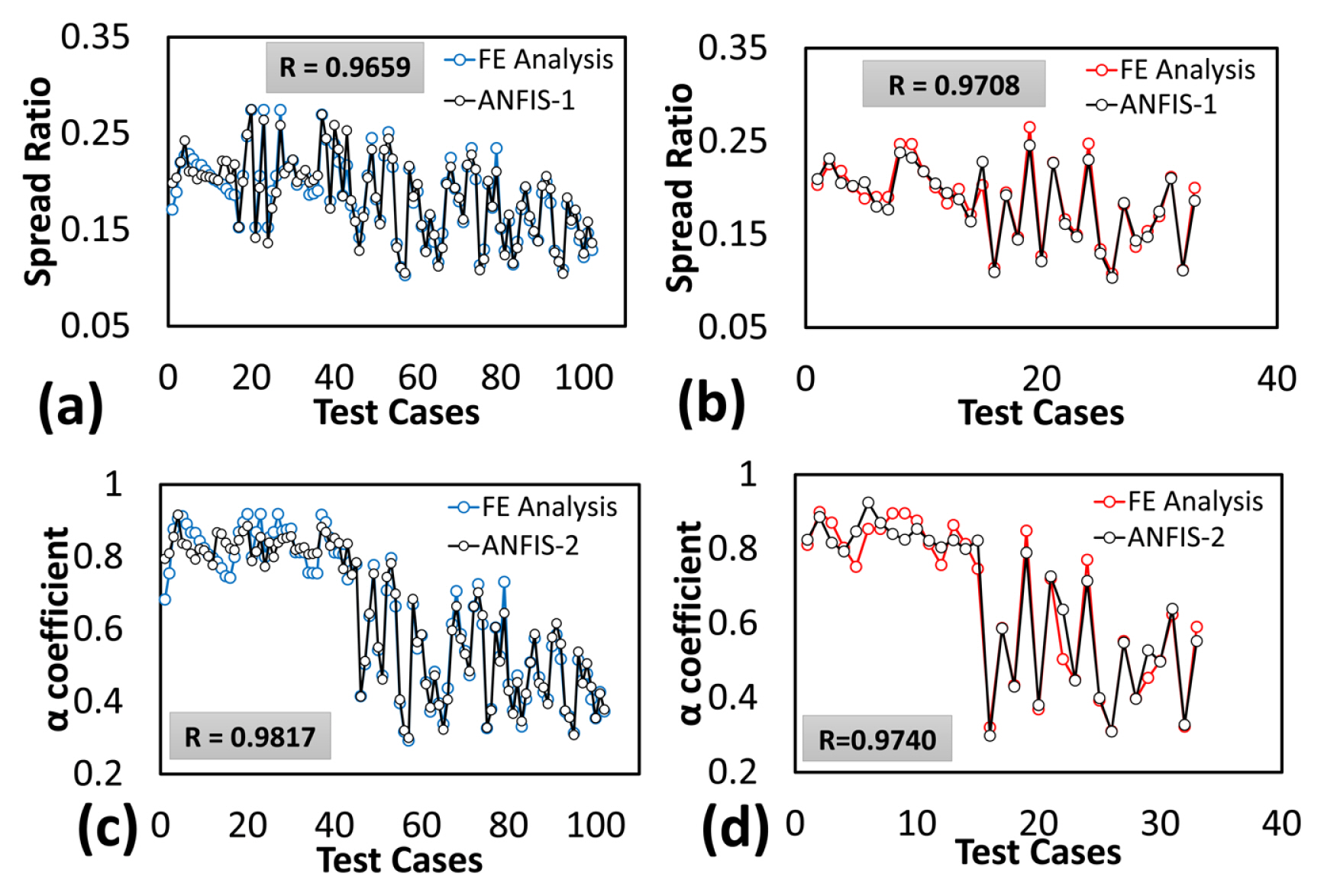
Fig.┬Ā16The relative effect of input parameters on the material width after rolling for oval and round caliber by using the ANFIS model 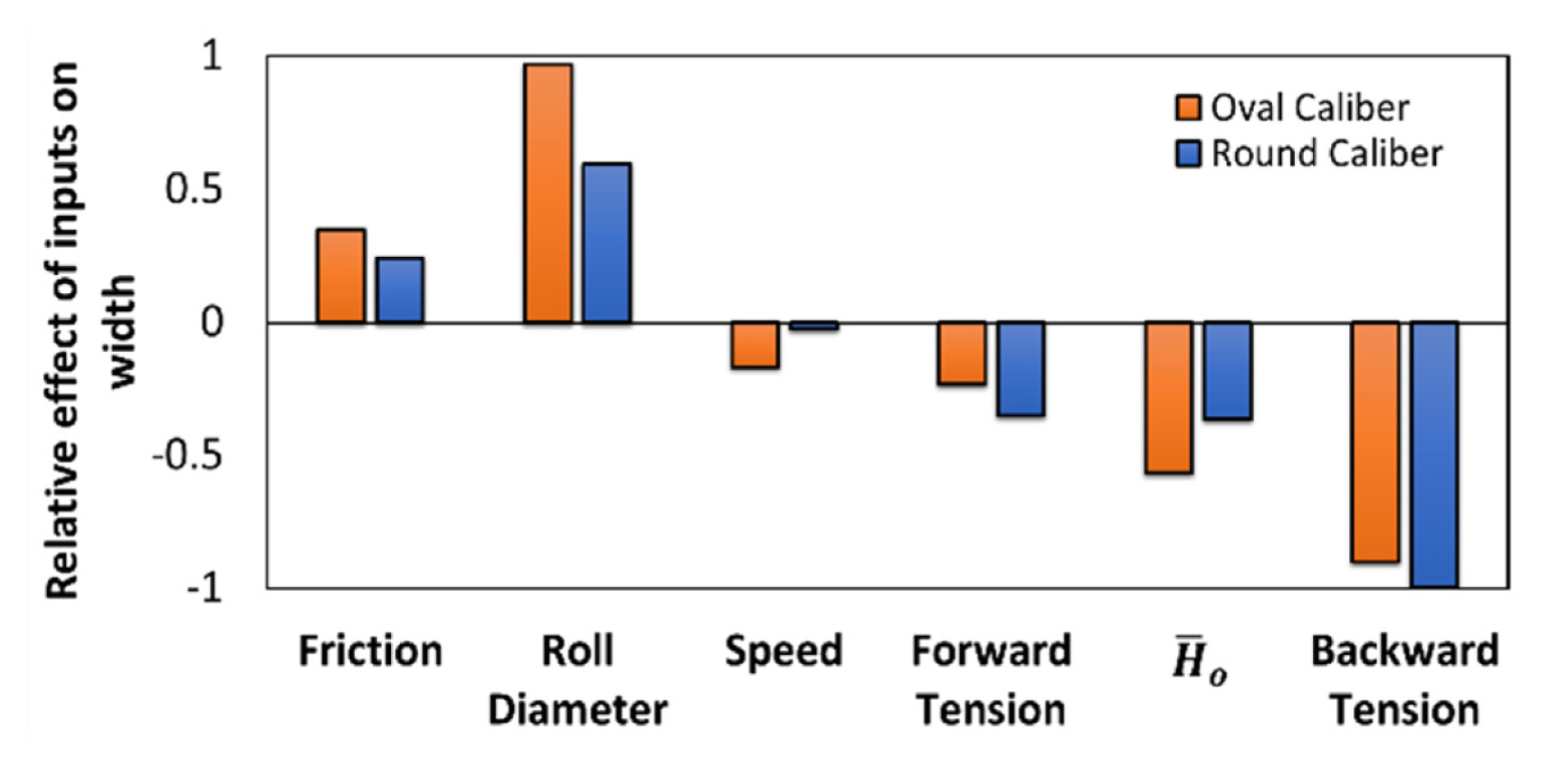
Fig.┬Ā17The effect of input parameters on the material width after rolling for (a) Oval caliber and (b) Round caliber by using ANFIS model 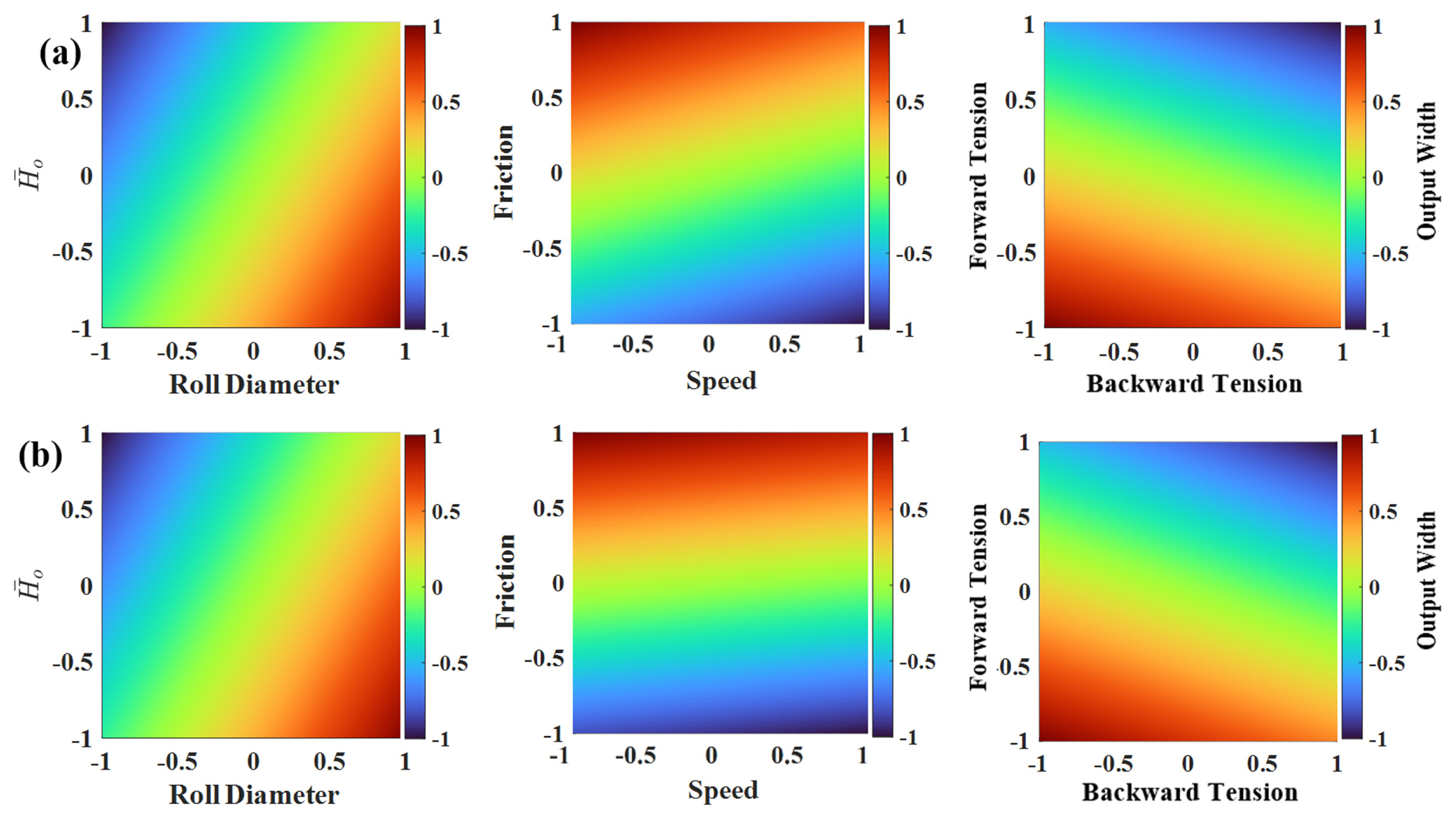
Fig.┬Ā18(a) The six-stand rolling used for the verification of the proposed model and (b) Comparison between the result of FE analysis and AI model 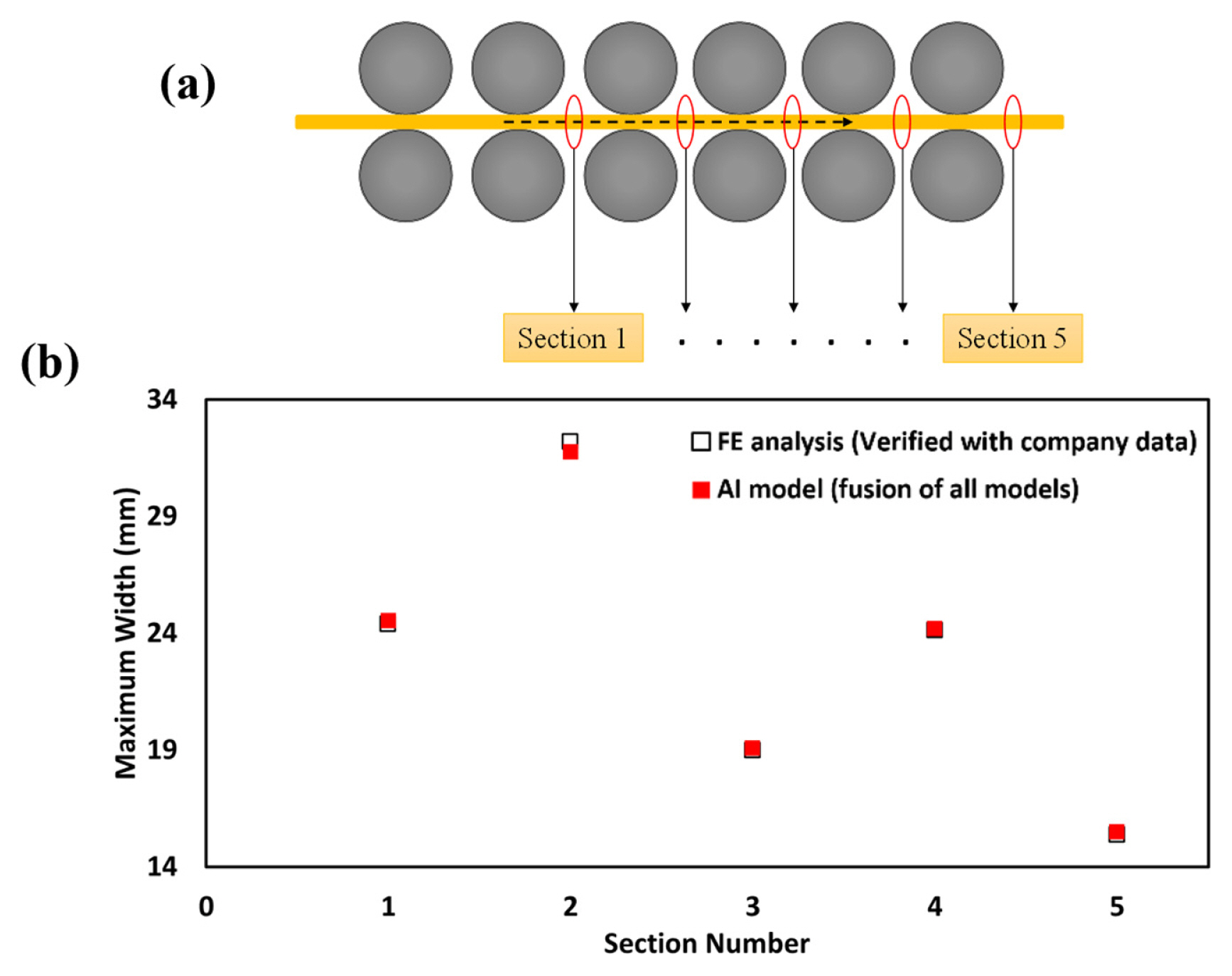
Table┬Ā1Johnson Cook parameters of the used steel
Table┬Ā2Physical properties of the used steel Table┬Ā3Different cases for simulation of wire roll rolling in one-stand rolling Table┬Ā4Input parameter ranges in one-stand rolling for the oval caliber
Table┬Ā5Case studies for simulation of wire roll rolling in three-stand rolling
Table┬Ā6Equations to make the input and output parameters dimensionless Table┬Ā7Inputs and outputs of all MLPs for the prediction of spread in oval and round caliber
Table┬Ā8Parameters of the MLP structure used to design all MLP models Table┬Ā9Parameters of the ANFIS structure used to design all ANFIS models Table┬Ā10The results of the proposed model for the prediction of width in six-stand rolling References1. Junquera, A. M. V., Gonz├Īlez, J. G., Balsera, J. M. V. & Montequ├Łn, V. R. (2020). A wire rod rolling mill digital twin for the simulation of the rolls replacement process. Proceedings, 63(1), 13.
2. ├¢verstam, H., Lundberg, S. E. & Jarl, M. (2003). Finite element modelling and laboratory simulation of high speed wire rod rolling in 3-roll stands. Steel Research International, 74(7), 431ŌĆō443.
3. Shinokura, T., & Takai, K. (1982). A new method for calculating spread in rod rolling. Journal of Applied Metalworking, 2(2), 94ŌĆō99.
4. Lee, Y., (2002). Prediction of the surface profile and area of the exit cross section of workpiece in round-oval-round pass sequence. ISIJ International, 42(7), 726ŌĆō735.
5. Lee, Y., & Choi, S. (2000). New approach for the prediction of stress free surface prof ile of a workpiece in rod rolling. ISIJ International, 40(6), 624ŌĆō626.
6. Hwang, J. K., (2020). Effect of cambered and oval-grooved roll on the strain distribution during the flat rolling process of a wire. Processes, 8(7), 876.
7. Inoue, T., (2010). Optimum pass design of bar rolling for producing bulk ultraf ine-grained steel by numerical simulation. Materials Science Forum, 654, 1561ŌĆō1564.
8. Hsiang, S. H., & Lin, S. L. (2007). Modeling and optimization of caliber rolling process. Journal of Manufacturing Science and Engineering, 129(1), 77ŌĆō83.
9. Yuan, S. Y., Zhang, L. W., Liao, S. L., Jiang, G. D., Yu, Y. S. & Qi, M. (2009). Simulation of deformation and temperature in multi-pass continuous rolling by three-dimensional FEM. Journal of Materials Processing Technology, 209(6), 2760ŌĆō2766.
10. Liao, S., Zhang, L., Yuan, S., Zhen, Y. & Guo, S. (2008). Modeling and finite element analysis of rod and wire steel rolling process. Journal of University of Science and Technology Beijing, Mineral, Metallurgy, Material, 15(4), 412ŌĆō419.
11. Siebel, E. (1923). Grundlagen zur berechnung des kraft-und arbeitsbedarfs beim schmieden und walzen.
12. Wusatowski, Z. (2013). Fundamentals of rolling. Technische Hochschule, Berlin: Elsevier.
13. Saito, Y., Moriga, M. & Kato, K. (1977). Calculation of spread and elongation of bars in rolling pass sequences, square-oval, square-diamond and round-oval. Tetsu-to-Hagane, 63(12), 1819ŌĆō1827.
14. Saito, Y., Takahashi, Y. & Kato, K. (1978). Calculation of spread, elongation, effective roll radius, roll force and torque when rolling in the square-diamond, square-oval and round-oval passes. Tetsu-to-Hagan├®, 64(2), 250ŌĆō259.
15. Shen, S., Guye, D., Ma, X., Yue, S. & Armanfard, N. (2022). Multistep networks for roll force prediction in hot strip rolling mill. Machine Learning with Applications, 7, 100245.
16. Bagheripoor, M., & Bisadi, H. (2013). Application of artificial neural networks for the prediction of roll force and roll torque in hot strip rolling process. Applied Mathematical Modelling, 37(7), 4593ŌĆō4607.
17. Wang, Z., Zhang, D., Gong, D. & Peng, W. (2019). A new data-driven roll force and roll torque model based on FEM and hybrid PSO-ELM for hot strip rolling. ISIJ International, 59(9), 1604ŌĆō1613.
18. DAL, , & Talamantes-Silva, J. (2003). Roll force and torque prediction using neural network and finite element modelling. ISIJ International, 43(12), 1957ŌĆō1966.
19. Li, X., Luan, F. & Wu, Y. (2020). A comparative assessment of six machine learning models for prediction of bending force in hot strip rolling process. Metals, 10(5), 685.
20. Wang, Z. H., Gong, D. Y., Li, X., Li, G. T. & Zhang, D. H. (2017). Prediction of bending force in the hot strip rolling process using artificial neural network and genetic algorithm (ANN-GA). The International Journal of Advanced Manufacturing Technology, 93(9), 3325ŌĆō3338.
21. Huang, Y., Zhou, X. & Gao, Z. (2022). Thickness prediction of thin strip cold rolling based on VBGM-RBF. The International Journal of Advanced Manufacturing Technology, 120(9), 5865ŌĆō5884.
22. Sui, X., & Lv, Z. (2016). Prediction of the mechanical properties of hot rolling products by using attribute reduction ELM. The International Journal of Advanced Manufacturing Technology, 85(5), 1395ŌĆō1403.
23. Wang, P., Huang, Z. Y., Zhang, M. Y. & Zhao, X. W. (2008). Mechanical property prediction of strip model based on PSO-BP neural network. Journal of Iron and Steel Research International, 15(3), 87ŌĆō91.
24. Liu, J., Song, S., Wang, J., Balaiti, M., Song, N. & Li, S. (2022). Flatness prediction of cold rolled strip based on deep neural network with improved activation function. Sensors, 22(2), 656.
25. John, S., Sikdar, S., Swamy, P. K., Das, S. & Maity, B. (2008). Hybrid neural-GA model to predict and minimise flatness value of hot rolled strips. Journal of Materials Processing Technology, 195(1ŌĆō3), 314ŌĆō320.
26. Al-Mahasneh, M., Aljarrah, M., Rababah, T. & AluŌĆÖdatt, M. (2016). Application of hybrid neural fuzzy system (ANFIS) in food processing and technology. Food Engineering Reviews, 8(3), 351ŌĆō366.
27. Huang, M. L., Hung, Y. H., Lee, W. M., Li, R. K. & Wang, T. H. (2012). Usage of case-based reasoning, neural network and adaptive neuro-fuzzy inference system classif ication techniques in breast cancer dataset classif ication diagnosis. Journal of Medical Systems, 36(2), 407ŌĆō414.
28. Riahifar, R., & Serajzadeh, S. (2007). Three-dimensional model for hot rolling of aluminum alloys. Materials & Design, 28(8), 2366ŌĆō2372.
29. Wang, M., Yang, H., Sun, Z. C. & Guo, L. G. (2009). Analysis of coupled mechanical and thermal behaviors in hot rolling of large rings of titanium alloy using 3D dynamic explicit FEM. Journal of Materials Processing Technology, 209(7), 3384ŌĆō3395.
30. Gornyakov, V., Sun, Y., Ding, J. & Williams, S. (2021). Computationally efficient models of high pressure rolling for wire arc additively manufactured components. Applied Sciences, 11(1), 402.
31. Nioi, M., Pinna, C., Celotto, S., Swart, E., Farrugia, D., Husain, Z. & Ghadbeigi, H. (2019). Finite element modelling of surface defect evolution during hot rolling of silicon steel. Journal of Materials Processing Technology, 268, 181ŌĆō191.
32. Johnson, G. R., (1983). A constitutive model and data for materials subjected to large strains, high strain rates, and high temperatures. In: Proceedings of the 7th International Symposium on Ballistics; pp 541ŌĆō547.
33. Min, J. H., Kwon, H. C., Lee, Y., Woo, J. S. & Im, Y. T. (2003). Analytical model for prediction of deformed shape in three-roll rolling process. Journal of Materials Processing Technology, 140(1ŌĆō3), 471ŌĆō477.
34. Shibahara, T., Misaka, Y., Kono, T., Koriki, M. & Takemoto, H. (1981). Edger set-up model at roughing train in hot strip mill. Tetsu-to-Hagane, 67(15), 2509ŌĆō2515.
35. Gardner, M. W., & Dorling, S. R. (1998). Artificial neural networks (the multilayer perceptron)-A review of applications in the atmospheric sciences. Atmospheric Environment, 32(14ŌĆō15), 2627ŌĆō2636.
36. Rumelhart, D. E., Hinton, G. E. & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature, 323(6088), 533ŌĆō536.
37. Najm, S. M., & Paniti, I. (2021). Artif icial neural network for modeling and investigating the effects of forming tool characteristics on the accuracy and formability of thin aluminum alloy blanks when using SPIF. The International Journal of Advanced Manufacturing Technology, 114(9), 2591ŌĆō2615.
38. Nguyen, D., & Widrow, B. (1990). Improving the learning speed of 2-layer neural networks by choosing initial values of the adaptive weights. IJCNN International Joint Conference on Neural Networks, 3, 21ŌĆō26.
39. Zadeh, L. A.Klir, G. J. & Yuan, B. (1996). Fuzzy sets, fuzzy logic, and fuzzy systems: Selected papers. World Scientific.
40. Jang, J. S., (1993). ANFIS: Adaptive-network-based fuzzy inference system. IEEE Transactions on Systems, Man, and Cybernetics, 23(3), 665ŌĆō685.
41. Takagi, T., & Sugeno, M. (1985). Fuzzy identification of systems and its applications to modeling and control. IEEE Transactions on Systems, Man, and Cybernetics, SMC, 15(1), 116ŌĆō132.
42. Pradhan, R., Pathak, K. K. & Singh, V. P. (2011). Application of neural network in prediction financial viability. International Journal of Soft Computing and Engineering (IJSCE), 1(2), 41ŌĆō45.
43. Raja, P., & Pahat, B. (2016). A review of training methods of ANFIS for applications in business and economics. International Journal of u-and e-Service, Science and Technology, 9(7), 165ŌĆō172.
Biography
Soheil Amani is a Ph.D. candidate in the Department of Mechanical and Manufacturing Engineering, University of Calgary. His research interest is machine learning, FE analysis, manufacturing, and vibration.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



 E-mail
E-mail Print
Print facebook
facebook twitter
twitter Linkedin
Linkedin google+
google+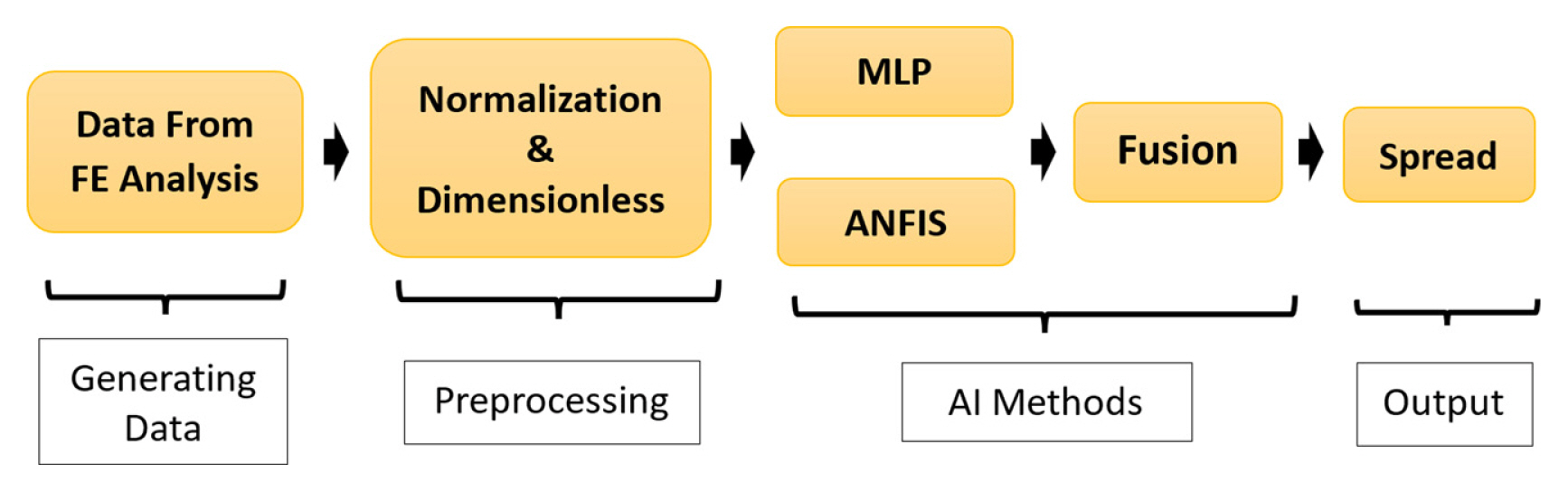


 PDF Links
PDF Links PubReader
PubReader Full text via DOI
Full text via DOI Download Citation
Download Citation  CrossRef TDM
CrossRef TDM

