1 Introduction
Computing the fundamental properties of state-of-the-art materials with high-precision and acceptable computational cost has long been a goal in the field of computational materials science [1–6]. By understanding the atomistic and electronic behaviors of target materials under various thermodynamical conditions, material properties, such as lattice constants, elastic properties, and diffusion behaviors, can be investigated. Consequently, this can provide an understanding of the working mechanism, and the obtained properties can be further used as inputs for materials informatics and artificial-intelligence-based approaches.
Molecular dynamics (MD) simulations have been extensively used toward this end, and their exceptional transferability and practical applicability have been proven [7]. MD simulations are advantageous because they define simplified functionals (i.e., force fields) by mimicking the potential energy surface from first-principles calculations, thereby ensuring considerable reduction in computational costs while achieving acceptable accuracy. In addition, they obtain atomic structure changes and energetics with respect to the time and thermodynamical conditions (i.e., temperature and pressure). However, a sophisticated parametrization process needs to be performed to represent the target of systems properly, and the constructed force fields are applicable only to certain systems; therefore, their applicability is largely limited. Furthermore, atomic behaviors and properties are normally valid only for pristine structures; thus, MD simulations may not be accurate for slab, cluster, and defective systems [8,9]. In contrast, the density functional theory (DFT), an ab initio method that is based on the calculation of the electronic nature of structures, exhibits exceptional accuracy for understanding the behaviors of materials. This method has been verified and implemented for various physical and chemical systems, including bulk, surface, and cluster structures [10–13]. However, owing to its high computational cost, its use has largely been restricted to computing the transport, thermal, and mechanical properties of various types of materials.
With regard to resolving the issues faced with existing calculation methods, the use of machine-learning- and neural-network-based interatomic potentials (MLIP and NNIP, respectively) of materials has exhibited exceptional transferability, accuracy, and generality [2,14,15]. Such potentials are used primarily to train the most reliable results from first-principles calculations by correlating the energy and atomic configuration and then implementing them for regression tasks on the total energy prediction. Thus, accurate quantum mechanics calculations can be performed with few computational resources. For example, Behler and Parrinello developed the neural network potential (NNP) [9,16,17] and confirmed its excellent applicability for various systems, such as silicon, lithium, and germanium bulk [8]; alloy structures [18,19]; and clusters of ZnSe structures [20]. The Gaussian approximation potential (GAP) uses a Gaussian process regressor for various systems, such as oxides [21], carbon nanostructures [22], and amorphous structures [23]. However, this approach naturally requires more computational resources, and therefore, it has limited applications [9]. The moment tensor potential (MTP) is another popular tool for constructing MLIPs; it uses polynomial-like functions for linear regression. Compared with MLIPs, it intrinsically has a good balance between the construction of very accurate potentials and the minimization of the computational cost [15]. MTPs have been successfully applied to multiscale modeling for predicting the mechanical properties of graphene/borophene heterostructures [24], elastic properties of multielement alloys [25], transport properties [26], solution enthalpy and diffusivity [27], and phase diagram of alloys [28]. In addition, MTP has been used for investigating the interfacial behavior of sulfide type of SSEs and Li diffusion [29].
In this study, MTP-based force fields are generated to investigate the fundamental behaviors of inorganic Li-ion solid-state electrolytes (SSEs). SSEs are considered promising components for next-generation Li-ion batteries because their lack of liquid electrolytes eliminates the risk of flammability, and they exhibit increased energy density and structural stability [30–32]. However, SSEs have lower ionic conductivity compared to that of liquid electrolytes; this has limited their broad commercialization [33]. Furthermore, the interface between electrode and electrolytes plays a key role in determining the performance and stability of the batteries. [34] More specifically, it is critical that from the manufacturing perspective, maintaining the solid physical contact of SSEs to the electrode could minimize the void and the crack generation [35]. Therefore, finding superionic SSEs is crucial for developing solid-state batteries; however, a reliable database of SSE properties is currently unavailable. This is because considerable computational resources are required for constructing such a database; usually, weeks are required for computations on one structure. Therefore, an alternative model that can reduce the computational time while providing good accuracy is needed; in this regard, MLIP may be promising owing to its functionality.
In this respect, the MTP method is used for developing a force field that describes the atomistic behaviors of well-known SSE structures, such as Li-Ge-P-X′ and Li-X″-P-S structures, where X′ = O, S, or Se and X″ = Ge, Si, or Sn. Ab initio molecular dynamics (AIMD) simulations are performed for constructing the training and validation databases. Subsequently, the accuracy of the developed MTP method is demonstrated by obtaining the structural, elastic, and diffusion properties of SSEs under various thermodynamical conditions.
2 Methods
2.1 Database Construction
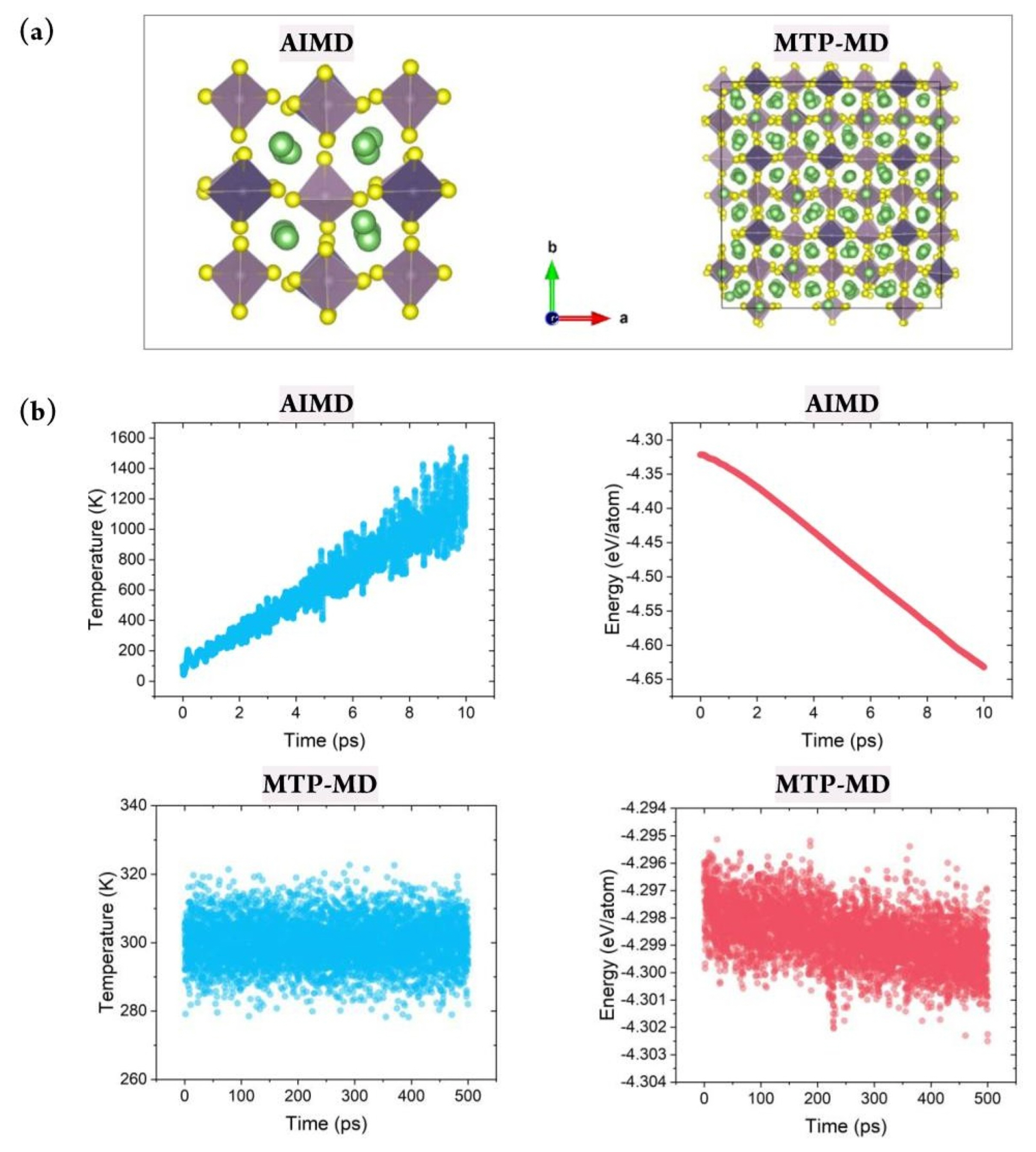
Fig. 1 shows the overall process of constructing the database for MTP training and applying it for calculating the ionic conductivity using MTP-MD. First, for constructing the MLIP, a training database containing the atomic structure and corresponding energy value must be constructed. For this purpose, the atomic configurations of Li-Ge-P-X′ and Li-X″-P-S structures, where X′ = O, S, or Se and X″ = Ge, Si, or Sn, were constructed. These materials were chosen because they are well-known SSEs that exhibit exceptional Li-ion conductivity at room temperature and outstanding electrochemical properties [36]. The atomic configuration for each structure was constructed using 50 atoms with the space group of P42/nmc. Fig. 2(a) shows an atomic snapshot of Li10GeP2S12 (LGPS) as an example. Subsequently, AIMD was performed for 10 ps for each structure to generate training data. The temperature was first set as 100 K and subsequently increased gradually to 1,200 K under a canonical ensemble (NVT). Such a temperature change was applied to obtain various atomic structures to ensure that the trained MTP could predict the energy of given structures more accurately even under various thermodynamical conditions; this reduces the need for extrapolation.
Next, MTPs were trained for all structures using the MLIP package [15], with 80% and 20% of the database being used for training and validation, respectively. To equally select the training database during the temperature change, database selection was performed in a stratified manner. For MTP construction, the following parameters were used. Size of radial basis = 8; weights of energies, forces, and stresses = 1, 0.1, and 0.001, respectively; and cutoff radius = 5 Å. Next, for validating the accuracy of the trained MTP, MTP-MD was performed. To obtain the diffusion behavior of the Li-ion, the simulation was performed for 500 ps under the NVT ensemble. The atomic structure for MD was increased to 1350 atoms; for this purpose, the unit cell from DFT is expanded by 3 × 3 × 3 to 27 times more atoms than that in the case of AIMD. Fig. 2(a) shows this expanded atomic structure of LGPS as an example. The MTP-MD simulations were conducted at 300, 600, 800, and 900 K. Finally, the ionic conductivity of each system was calculated using the PyLAT package, a post-processing tool [37].
2.2 Calculation Details
The AIMD calculations were performed using the Vienna ab initio simulation package (VASP) [38,39]. The Perdew-Burke-Ernzerhof generalized gradient approximation [40] was used for the exchange-correlation functional. The plane-wave cutoff was set as 400 eV, gamma-point was used for k-point grid generation, and a time step of 2 fs was used; thus, 5,000 calculations were performed for database construction. An energy convergence criterion of 10−5 and 10−6 eV was used for AIMD and static DFT calculations, respectively. For computing the elastic tensor, the central difference with three displacements was applied with a step of 0.02 Å. The plane-wave cutoff for the static DFT and elastic constant calculation was set to 520 eV, and a 2 × 2 × 2 k-point grid was employed. For structural minimization, the structure was relaxed until the force was less than 0.03 eV/Å. To conduct MTP-MD for production, the large-scale atomic/ molecular massively parallel simulator (LAMMPS) [7] was used with a time step of 2 fs. For elastic constant calculations, the fourth rank tensor of the elastic constant matrix at zero temperature (for comparison with the DFT calculations) was constructed based on a previous reference [41].
3 Results and Discussions
3.1 MTP Construction
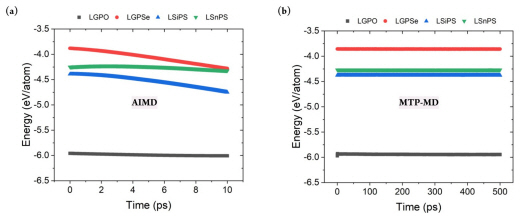
Constructing a reliable training database is critical for properly representing the system of interest under various thermodynamical conditions. This can be achieved by considering various atomic structure variations with respect to the temperature change. Fig. 2(b) demonstrates that during AIMD simulations of LGPS, the temperature was gradually increased from 100 to 1,200 K. Further, the thermal vibration became more significant; this was natural and beneficial for generating various atomic configurations at higher temperatures. In addition, the energy value gradually decreased during AIMD simulation, and no nonphysical energy change, such as overshooting or nonmonotonic behavior, was observed; this confirmed the reliability of the database construction process. Fig. S1 shows the total energy change for the other four structures during AIMD. It clearly exhibits a behavior similar to that of LGPS, thus verifying the reliability of the training database construction process.
After constructing the MTP, MTP-MD was performed to confirm whether the constructed potential could control the atomistic behaviors under various thermodynamical conditions. MD simulations often become unstable depending on the time step, temperature, and pressure because the predefined functional could be invalid for a certain region of atomic coordinates or under other given conditions. In this respect, MD simulations should be performed for sufficient time to confirm the stability of the implemented force field. Fig. 2(b) (bottom) clearly demonstrates that during 500 ps of MTP-MD simulations, the properties of the LGPS structure could be properly computed without any undesirable behaviors. For example, at 300 K, the thermal vibration was within 10 K, and this was sufficiently small compared with the AIMD results. In addition, a negligible total energy change was observed, and the average value decreased from −4.298 to only −4.299 eV/ atom when MD simulations were performed for a sufficiently long time at the same temperature. Fig. S1(b) shows the total energy change for the other four structures, and it confirms the stability of the developed potentials. Evidently, each MTP ran stably, and no unwanted thermal effects or abnormal energy change was observed.
3.2 MTP Prediction Accuracy
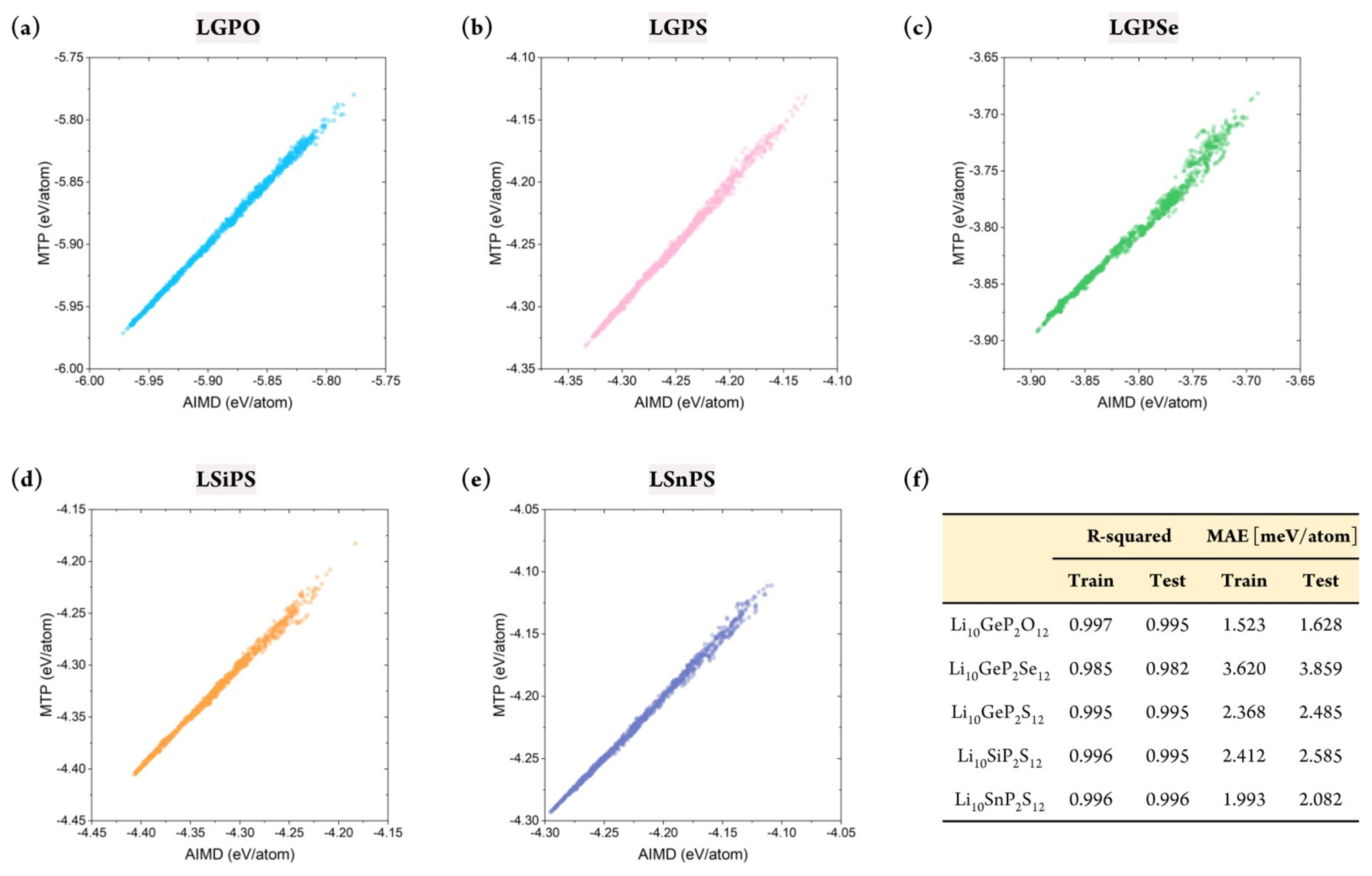
Although the stability of the constructed MTP has been confirmed, confirming whether it can accurately predict the energy of the target structures is critical. This is because the primary purpose of developing the MLIP is to mimic the potential energy surface of the first-principle calculations. In this respect, the database was divided into a training set (80%) and test/validation set (20%). Essentially, the MTP was trained to correlate the structure and the energy based on the training set, and validation was performed using the test set. Because the database was constructed in a timely manner, stratified sampling was performed to ensure that the training set included all temperature ranges. In addition, to measure the sampling uncertainty, the training set was constructed from differing random states with 20 times.
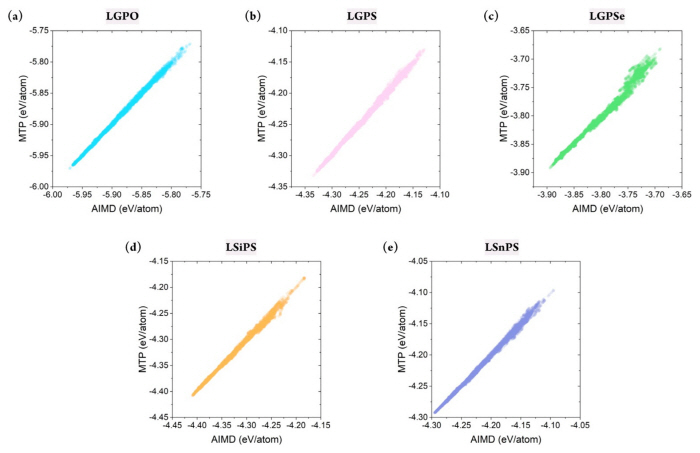
Figs. S2 and 3 show the prediction accuracy of the constructed MTP for the training and test sets, respectively. This result confirmed that the MTPs for all five structures could predict the energy of the systems with remarkable accuracy. Furthermore, the database did not contain any large error, which indicated that the MTP could properly represent the energy surface of all structures under varying thermodynamical conditions. Critically, the training accuracy could be obtained easily; more importantly, the outstanding accuracy of the test set indicated that extrapolation behavior was not observed. Fig. 3(f ) shows that the R2 value for the training set varied from 0.985 to 0.997, with a mean absolute error (MAE) of 1.523–3.620 meV/atom. Further, for the test set, the R2 value was approximately 0.982–0.996, with an MAE value of 1.628–3.859 meV/atom. Although reduced prediction accuracy is normally expected for the test set, such behavior was hardly observed in this study. In addition, the prediction uncertainty for all structures with respect to different sampling states was only approximately 0.001 and 0.1 meV/atom for R2 and MAE, respectively, further confirming the stability of the constructed MTPs. In summary, the constructed MTP can work stably to predict the energy of the target systems under various thermodynamical conditions with accuracy comparable to that of AIMD.
The above results confirmed the energy predicting capability of MTPs. Next, they must be implemented to calculate the fundamental material properties of each structure as MLIP can be used to perform structural relaxation to obtain an energetically minimized structure. In addition, the energy of the system varies with respect to the change in the bond distance, and it is directly related to the elastic properties. In this regard, the lattice constants and bulk modulus of all structures were calculated, and the results were compared with the DFT outcomes. As presented in Table 1, the lattice parameters of all SSEs as obtained using MTP-MD were comparable to those obtained using static DFT calculations. Furthermore, the bulk modulus calculated using MTP-MD was within approximately 5% of the value obtained using DFT calculations. These results suggest that MTP can accurately represent the structural changes of the target structures with accuracy comparable to that of DFT. In addition, such a capability can be further implemented for screening ideal SSEs because the electrochemical stability window and mechanical properties are also critical criteria [30,31]. Since those properties are closely related to the energy change for given structures, implementing MTP can greatly reduce the computation cost.
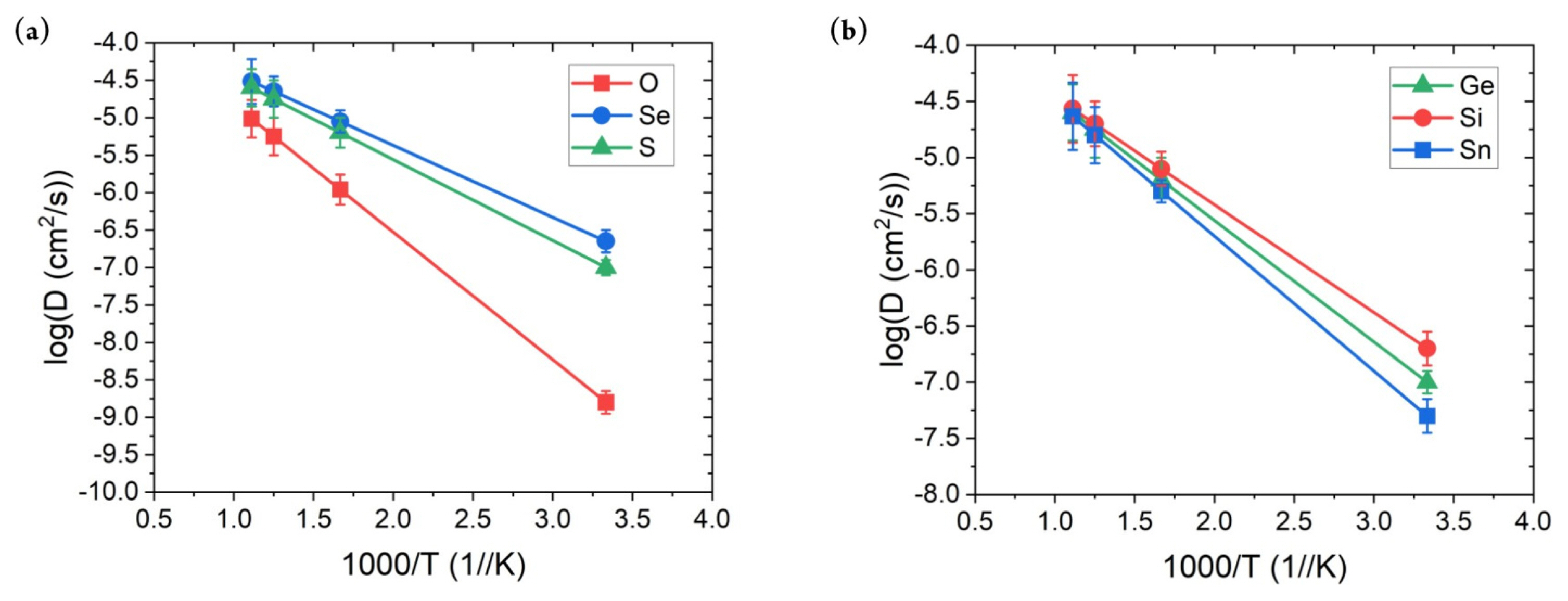
Finally, the Li-ion ionic conductivity measurement at room temperature for SSEs was performed. As mentioned above, the calculation of this property is the primary bottleneck because it requires weeks to complete. In addition, the diffusion behavior of the ion is a dynamic property; therefore, previously confirmed properties do not guarantee that the constructed MTPs can accurately describe such behavior. Fig. 4 shows the MTP-calculated diffusivity values with respect to the temperature. Overall, they exhibited a linear increase with temperature, with only a small error; moreover, no abnormal behavior was observed. The error of around log 0.1 cm2/s is obtained for all of the structures with the considered range of temperatures. This indicates that the developed MTP stability captures the diffusion behavior of the considered SSE materials. Based on this result, the ionic conductivity values were calculated, as presented in Table 2. AIMD results were adopted from a previous reference [36]. First, the ionic conductivity obtained using MTP-MD generally agreed with that obtained using AIMD simulations. The MAE was only 3.126 mS/cm, with maximum and minimum errors of 4.75 and −2.15 mS/cm, respectively. In addition, Pearson’s correlation coefficient between the ionic conductivity of MTP-MD and AIMD was 0.965, which indicated their high linear correlation. Although the percentage error for LGPO structure is significant, considering the MAE value of the current result, such error would be the limitation of the MTP method. More importantly, the general trend and the rank of the materials are matching well with the AIMD results so implementing MTP is still a useful tool for prediction of ionic conductivity of SSE materials.
The ultimate goal of implementing MTP-MD is to obtain the material properties with the same accuracy as AIMD but without the computational cost of SIMD. Thus far, we have confirmed that the developed potential can accurately capture the energy, structural information, and diffusion behavior of SSEs. In terms of computational cost, Table 1 presents how long the computations can be performed under a given time. In this study, we used a 16-core Intel Xeon Gold 6226R CPU processor for all computations. The results clearly verified that MTP-MD runs approximately three orders of magnitude faster than an AIMD. For example, the Li10GeP2Se12 (LGPSe) structure can be run at 1.03 ps/h using AIMD and at 2,272.7 ps/h using MTP-MD. Critically, the atomic structure of AIMD used only 50 atoms, whereas MTP-MD used 1,350 atoms. Therefore, we conducted MTP-MD simulations with 50 atoms for the LGPSe structure and determined that it now runs at 4,928.2 ps/h, further confirming the practical usability of the develop potential.
3.3 Future Research Directions
Although the current study clearly demonstrates the transferability and stability of the developed MTP for well-known SSE materials, further investigations and improvements are needed for enhancing its usability and generality from a practical viewpoint. First, the developed potentials in the current study are valid only for each structure; essentially, the potential for Li10GeP2O12 cannot be used for Li10SnP2S12. To improve the generality of the force fields, the potential must be able to describe structures, such as Li10Ge0.5Sn0.5P2O12. Moreover, MTP can be developed for describing all structures comprising Li-Ge-Sn-P-O. However, both cases require the construction of a much more extensive database because, as discussed, constructing a training database for only the target system is more straightforward for researchers. To improve the generality, a larger number of structures with different space group numbers and compositions should be considered, although this would dramatically increase the computational cost. Thus, an efficient database construction process is needed to avoid producing an unnecessary database during AIMD.
Second, although the purpose of developing the potential is to investigate various material properties of target structures, constructing a surrogate model would be more efficient in some cases. For example, because numerous databases are already available for inorganic solids [6,42], constructing force fields to compute their lattice constants, elastic properties, and vibrational properties would be inefficient. However, a well-constructed database for predicting the ionic conductivity is unavailable as considerable resources are required for performing the necessary computations or experiments. Therefore, developing a force field would be more appropriate in this case. This is because although it still requires the construction of an initial training database, the total amount of computational resources required will be much lesser than those required for obtaining the material properties themselves. Such factors should always be considered in advance when deciding a research direction to maximize the benefit of implementing the MLIP.
4 Conclusions
Herein, MTP was successfully developed for predicting the fundamental behaviors of SSE materials. Five different types of Li-ion SSEs were considered, and the constructed MTPs exhibited remarkable accuracy for calculating the total energy, lattice constant, and bulk modulus of all structures. To further confirm the transferability of the developed potentials, the ionic conductivity at room temperature was calculated using MTP-MD simulations for different simulation temperatures. The results clearly confirm that the obtained values have an accuracy comparable to that of values obtained using AIMD simulations. Further, MTPs require a simulation time that is three orders of magnitude smaller. We believe that the current study can guide future directions of research on material properties using MLIP, which provides accuracy comparable to that of DFT and AIMD, while requiring much fewer computational resources.



 E-mail
E-mail Print
Print facebook
facebook twitter
twitter Linkedin
Linkedin google+
google+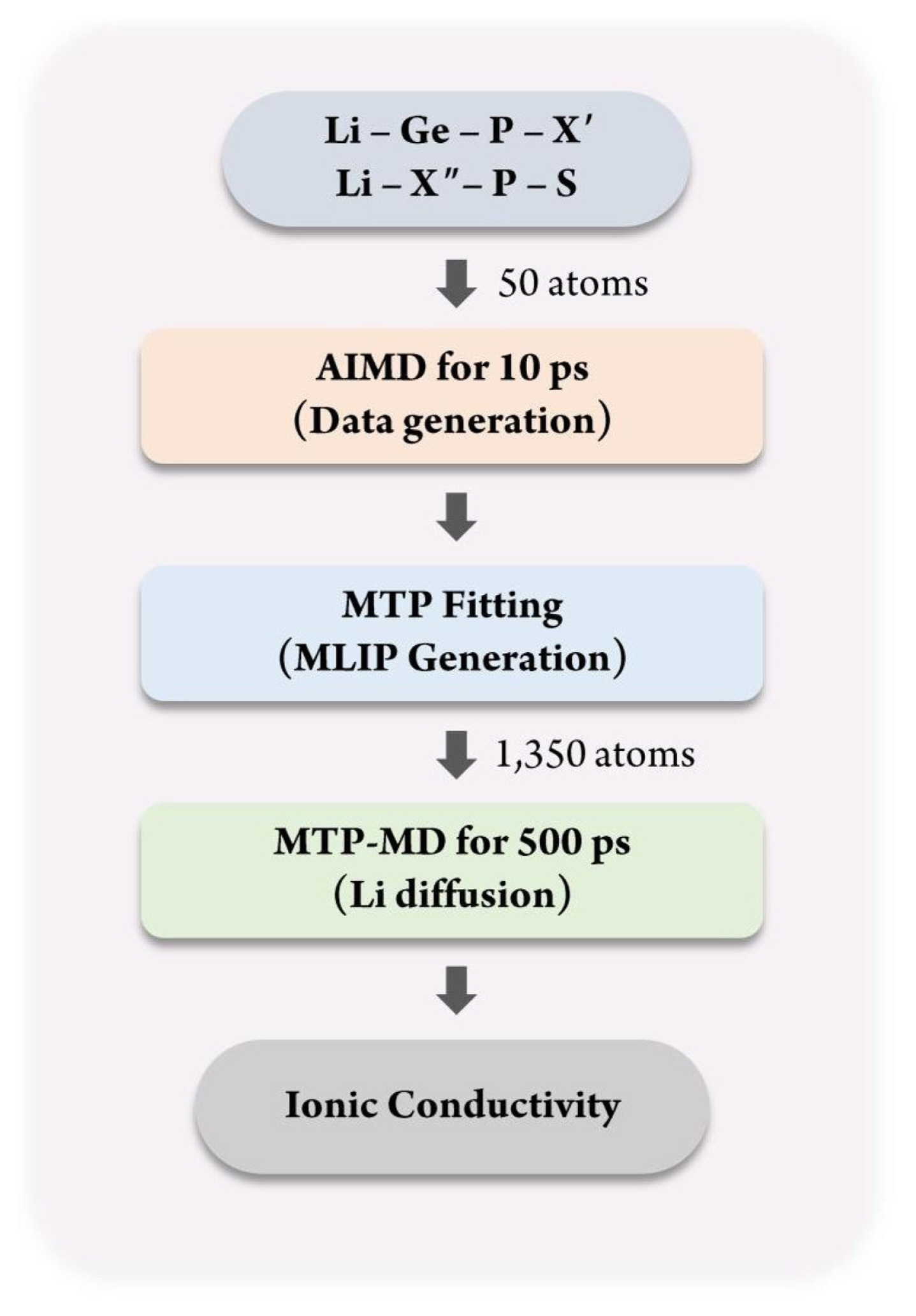

 PDF Links
PDF Links PubReader
PubReader Full text via DOI
Full text via DOI Download Citation
Download Citation  CrossRef TDM
CrossRef TDM



